Question

【题目】（本小题满分12分）△ABC中，角A，B，C所对的边分别为a，b，c．已知a＝3，cos A＝，B＝A＋．

（1）求b的值；

（2）求△ABC的面积．

Answer 1

【答案】（1） ． （2）

【解析】

试题分析：（1） 已知两角及对边求另一对边，应该利用正弦定理，在△ABC中，sin A＝ ，sin B＝sin＝cos A＝，由正弦定理可得，b＝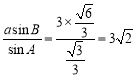

（2）三角形面积公式选用S＝absin C，则需求出sin C，sin C＝sin[π－（A＋B）] ＝sin（A＋B） ＝sin Acos B＋cos Asin B＝×＋×＝．因此△ABC的面积S＝absin C＝×3××＝．

试题解析：（1）在△ABC中，

由题意知，sin A＝

又因为B＝A＋，

所以sin B＝sin＝cos A＝

由正弦定理可得，b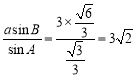＝ 6分

（2）由B＝A＋得cos B＝cos＝－sin A＝－．

由A＋B＋C＝π，得C＝π－（A＋B），

所以sin C＝sin[π－（A＋B）]

＝sin（A＋B）

＝sin Acos B＋cos Asin B

＝×＋×

＝．

因此△ABC的面积S＝absin C＝×3××＝． 12分