题目内容
(本题满分14分) 在△ABC中，角A，B，C所对的边分别为a，b，c，已知
tan (A＋B)＝2．
(Ⅰ) 求sin C的值；
(Ⅱ) 当a＝1，c＝
时，求b的值．
tan (A＋B)＝2．
(Ⅰ) 求sin C的值；
(Ⅱ) 当a＝1，c＝
时，求b的值．(Ⅰ) 解：由题设得tan C＝－2，从而sinC＝
．
(Ⅱ) 解：由正弦定理及sinC＝得sin A＝
，
sin B＝sin (A＋C)＝sin A cos C＋sin C cos A
＝
＝
，
再由正弦定理b＝
＝
．
．(Ⅱ) 解：由正弦定理及sinC＝
得sin A＝，sin B＝sin (A＋C)＝sin A cos C＋sin C cos A
＝
＝
，再由正弦定理b＝
＝． 略
练习册系列答案
阅读快车系列答案
相关题目
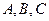是一条直路上的三点，
,
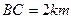，从三点分别遥望塔
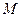,在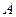
处看见塔在北偏东
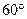，在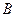
处看见塔在正东方向，在
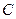处看见塔在南偏东
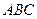的最短距离。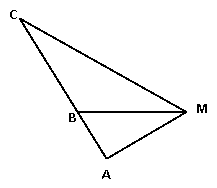
中，
，
，
，则
（ ）
相距9海里的C处有一艘走私船，正沿南偏东75
中，
，
，
．
、
的值； （2）求
的值
中，角
的对边分别为
已知
.
的值；
,求
中，角A、B、C的对边分别为a、b、c, A=2B.
，求
的值；
的取值范围.
中，
，则角B= ▲ 
b＝
,则a、b的等比中项为