题目内容
(2013•连云港一模)在平面直角坐标系xOy中,已知圆(x-1)2+(y-1)2=4,C为圆心,点P为圆上任意一点,则
•
的最大值为
| OP |
| CP |
2
+4
| 2 |
2
+4
.| 2 |
分析:根据向量加法的三角形法则和数量积运算性质,化简得
•
=
•
+
2.由点P是圆C(x-1)2+(y-1)2=4上的点得
2=4,而当
与
方向相同时
•
的最大值为|
|•|
|=2
,因此即可算出
•
的最大值.
| OP |
| CP |
| OC |
| CP |
| CP |
| CP |
| OC |
| CP |
| OC |
| CP |
| OC |
| CP |
| 2 |
| OP |
| CP |
解答:解: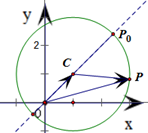 ∵
∵
=
+
∴
•
=(
+
)•
=
•
+
2
∵点P是圆C(x-1)2+(y-1)2=4上的点
∴
的长度等于圆C的半径,即|
|=2,可得
2=|
|2=4
又∵当
与
方向相同时,
•
=|
|•|
|取得最大值
∴当P点在OC延长线上时,即点P与P0(1+
,1+
)重合时,
•
的最大值为|
|•|
|=2
因此
•
的最大值为2
+4
故选:2
+4
 ∵
∵| OP |
| OC |
| CP |
∴
| OP |
| CP |
| OC |
| CP |
| CP |
| OC |
| CP |
| CP |
∵点P是圆C(x-1)2+(y-1)2=4上的点
∴
| CP |
| CP |
| CP |
| CP |
又∵当
| OC |
| CP |
| OC |
| CP |
| OC |
| CP |
∴当P点在OC延长线上时,即点P与P0(1+
| 2 |
| 2 |
| OC |
| CP |
| OC |
| CP |
| 2 |
因此
| OP |
| CP |
| 2 |
故选:2
| 2 |
点评:本题给出圆C上的动点P,求向量
•
的最大值,着重考查了平面向量数量积的定义及运算性质、圆的标准方程等知识,属于中档题.
| OP |
| CP |

练习册系列答案
相关题目