题目内容
设a、b、c为某一三角形三边长,求证:a2(b+c-a)+b2(c+a-b)+c2(a+b-c)≤3abc.
思路分析:运用排序原理,关键是弄出有序数组,通常从函数的单调性质去寻找,如f(x)=x2在R+单调递增,f(x)=![]() 在R+单调递减.
在R+单调递减.
证明:不妨设a≥b≥c,易证a(b+c-a)≤b(c+a-b)≤c(a+b-c).
由排序原理得a2(b+c-a)+b2(c+a-b)+c2(a+b-c)
≤a·b(c+a-b)+b·c(a+b-c)+c·a(b+c-a)=3abc.

练习册系列答案
相关题目
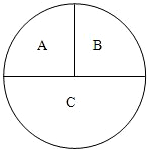 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.