题目内容
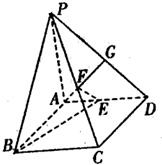
如图在四棱锥P﹣ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.
(I)求证:PB∥平面ACM;
(II)求证:MN⊥平面PAC;
(III)若 ,求平面FMN与平面ABCD所成二面角的余弦值.
,求平面FMN与平面ABCD所成二面角的余弦值.
(I)求证:PB∥平面ACM;
(II)求证:MN⊥平面PAC;
(III)若
 ,求平面FMN与平面ABCD所成二面角的余弦值.
,求平面FMN与平面ABCD所成二面角的余弦值. 
(I)证明:连接AC,BD,AM,MC,MO,MN,且AC∩BD=O
∵点O,M分别是PD,BD的中点
∴MO∥PB,PB 平面ACM
平面ACM
∴PB∥平面ACM.
(II)证明:∵PA⊥平面ABCD,BD 平面ABCD
平面ABCD
∴PA⊥BD
∵底面ABCD是正方形,
∴AC⊥BD
∵PA∩AC=A,
∴BD⊥平面PAC
在△PBD中,点M,N分别是PD,PB的中点,
∴MN∥BD ∴MN⊥平面PAC.
(III)解:PA⊥平面ABCD,底面ABCD是正方形,
故以A为原点,建立空间直角坐标系
由 可得
可得 
设平面MNF的法向量为 =(x,y,z)
=(x,y,z)
∵
∴ ,解得:
,解得:
令x=1,可得 =(1,1,5)
∵平面ABCD的法向量为
∴


∵点O,M分别是PD,BD的中点
∴MO∥PB,PB
 平面ACM
平面ACM ∴PB∥平面ACM.
(II)证明:∵PA⊥平面ABCD,BD
 平面ABCD
平面ABCD ∴PA⊥BD
∵底面ABCD是正方形,
∴AC⊥BD
∵PA∩AC=A,
∴BD⊥平面PAC
在△PBD中,点M,N分别是PD,PB的中点,
∴MN∥BD ∴MN⊥平面PAC.
(III)解:PA⊥平面ABCD,底面ABCD是正方形,
故以A为原点,建立空间直角坐标系
由
 可得
可得 
设平面MNF的法向量为
 =(x,y,z)
=(x,y,z)∵

∴
 ,解得:
,解得:
令x=1,可得 =(1,1,5)
∵平面ABCD的法向量为

∴




练习册系列答案
相关题目
 如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2
如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2 如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( )
如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( ) 如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点
如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点 如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形,
如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形, 如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.
如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.