题目内容
【题目】设函数![]() (
(![]() 是自然对数的底数).
是自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 内无极值,求
内无极值,求![]() 的取值范围;
的取值范围;
(3)设![]() ,求证:
,求证: ![]() 。
。
【答案】(1)![]() 在
在![]() ,
, ![]() 单调递增,在
单调递增,在![]() 单调递减(2)
单调递减(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)先对函数求导,再运用导数与函数的单调性之间的关系分析求解;(2)先将在![]() 问题进行转化,再分离参数,构造函数运用分类整合思想及导数知识分析求解;(3)依据题设条件运用数学归纳法进行推证:
问题进行转化,再分离参数,构造函数运用分类整合思想及导数知识分析求解;(3)依据题设条件运用数学归纳法进行推证:
解:(1)当![]() 时,
时, ![]()
所以![]()
当![]() 时,
时, ![]() 当
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]()
故![]() 在
在![]() ,
, ![]() 单调递增,在
单调递增,在![]() 单调递减
单调递减
(2)若![]() 在
在![]() 内无极值,则
内无极值,则![]() 在
在![]() 上单调,
上单调,
又![]()
①若![]() 在
在![]() 上递减,则
上递减,则![]() ,对
,对![]() 恒成立,于是有
恒成立,于是有
![]() ,令
,令![]() ,
,
下面证明![]() 在
在![]() 上单调递增:
上单调递增:
![]() 令
令![]() ,则
,则![]()
当![]() 时,
时, ![]() 单调递减,
单调递减, ![]()
![]() 在
在![]() 单调递增。
单调递增。
当![]() 时,由
时,由![]() 是增函数,得
是增函数,得![]() 。
。
由![]() ,得
,得![]() ;
;
②若![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,对
,对![]() 恒成立,于是
恒成立,于是
![]() ,当
,当![]() 时,由
时,由![]() 得
得![]() ,从而增函数
,从而增函数
![]() ,这样
,这样![]() 。综上得
。综上得![]()
(3)用数学归纳法证明 ①当![]() 时,
时, ![]() ,不等式成立;
,不等式成立;
②假设![]() 时不等式成立,即
时不等式成立,即![]() ,
,
当![]() 时,令
时,令
显然![]() ,由归纳假设,
,由归纳假设, 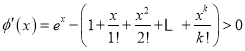 对
对![]() 成立,
成立,
所以 ![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时, ![]() ,即当
,即当![]()
时,不等式也成立。
综合①②![]() 时,不等式成立。
时,不等式成立。

练习册系列答案
相关题目