Question

已知正方形ABCD的边长为2，H是边DA的中点．在正方形ABCD内部随机取一点P，则满足|PH|＜

2

的概率为（　　）

• A．

  π

  8

• B．

  π

  8

  +

  1

  4

• C．

  π

  4

• D．

  π

  4

  +

  1

  4

Answer 1

分析：根据几何概型的概率计算公式，分别求出正方形的面积和满足|PH|＜

2

的正方形内部的点P的集合”的面积即可求出所求．

解答：解：（1）如图所示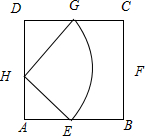，正方形的面积S_{正方形ABCD}=2×2=4．
设“满足|PH|＜

2

的正方形内部的点P的集合”为事件M，
则S（M）=S_△DGH+S_△AEH+S_扇形EGH=2×

1

2

×1×1+

1

2

×

2

×

π

2

×

2

=1+

π

2

，
∴P（M）=

1+ π 2

4

=

π

8

+

1

4

．
故满足|PH|＜

2

的概率为

π

8

+

1

4

．
故选B．

点评：本题主要考查了几何概型的概率，区域的面积和长度以及要求的事件的区域的面积和长度是解题的关键．属于基础题．