题目内容
已知 ,且
,且 .
.(1)求
 的值; (2)求cosβ的值.
的值; (2)求cosβ的值.
【答案】分析:(1)先化简 ,得到用正切表达的代数式,再代入
,得到用正切表达的代数式,再代入 求出值;
求出值;
(2)由于β=α+β-α,故可先求出α与α+β的正余弦值,再用余弦的差角公式将cosβ用α与α+β的正余弦值表示出来,然后求值;
解答:解 (1)∵ ,
,
∴ =
=
(2)∵α,β∈(0, ,
,
∴cosα= ,又sin(α+β)=
,又sin(α+β)=
则cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
=- ×
× +
+ ×
×
=-
点评:本题考查考查三角函数的化简求值,解题的关键是对三角函数的解析式化简,利用余弦的二倍角公式与正弦的和角公式进行变形,再由同角三角函数基本关系将代数式用正切表示出来,本题第二小题用到了角的变换,角的变换是探究已知与未知角的关系常用的方法
 ,得到用正切表达的代数式,再代入
,得到用正切表达的代数式,再代入 求出值;
求出值;(2)由于β=α+β-α,故可先求出α与α+β的正余弦值,再用余弦的差角公式将cosβ用α与α+β的正余弦值表示出来,然后求值;
解答:解 (1)∵
 ,
,∴
 =
=
(2)∵α,β∈(0,
 ,
,
∴cosα=
 ,又sin(α+β)=
,又sin(α+β)=
则cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα
=-
 ×
× +
+ ×
×
=-

点评:本题考查考查三角函数的化简求值,解题的关键是对三角函数的解析式化简,利用余弦的二倍角公式与正弦的和角公式进行变形,再由同角三角函数基本关系将代数式用正切表示出来,本题第二小题用到了角的变换,角的变换是探究已知与未知角的关系常用的方法

练习册系列答案
相关题目
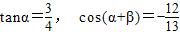 ,且
,且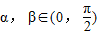 .
.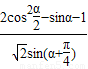 的值; (2)求cosβ的值.
的值; (2)求cosβ的值.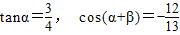 ,且
,且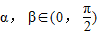 .
.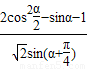 的值; (2)求cosβ的值.
的值; (2)求cosβ的值.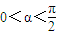 ,且
,且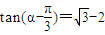 .
.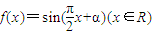 ,求f(1)+f(2)+f(3)+…+f(2012)的值.
,求f(1)+f(2)+f(3)+…+f(2012)的值. 且
且 ,
, 的取值范围;
的取值范围; 的最大值和最小值。
的最大值和最小值。