题目内容
下列说法正确的是
- A.?x∈(0,π),均有sinx>cosx
- B.命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0”
- C.“a=0”是“函数f(x)=x3+ax2+x为奇函数”的充要条件
- D.?x∈R,使得
 成立
成立
C
分析:选项A,可举x= 说明错误;选项B,正确的应为“?x∈R,均有x2+x+1≥0”;选项C,可由奇函数的性质说明正确;选项D,由三角函数的知识可得sinx+cosx的值域为[
说明错误;选项B,正确的应为“?x∈R,均有x2+x+1≥0”;选项C,可由奇函数的性质说明正确;选项D,由三角函数的知识可得sinx+cosx的值域为[ ,
, ],因为
],因为 ∉[
∉[ ,
, ],故错误.
],故错误.
解答:选项A,当x= 时,sin
时,sin =
= ,cos
,cos =
= ,显然有x∈(0,π),但sinx<cosx,故A错误;
,显然有x∈(0,π),但sinx<cosx,故A错误;
选项B,命题“?x∈R使得x2+x+1<0”的否定应该为:“?x∈R,均有x2+x+1≥0”,故B错误;
选项C,当a=0时,数f(x)=x3+x显然为奇函数,当f(x)=x3+ax2+x为奇函数时,由f(0)=0可得a=0,
故“a=0”是“函数f(x)=x3+ax2+x为奇函数”的充要条件,故C正确;
选项D,sinx+cosx= sin(x+
sin(x+ )∈[
)∈[ ,
, ],因为
],因为 ∉[
∉[ ,
, ],
],
故不存在x∈R,使 ,故D错误.
,故D错误.
故选C
点评:本题考查命题真假的判断,涉及函数的奇偶性和三角函数的性质以及特称命题的否定,属基础题.
分析:选项A,可举x=
 说明错误;选项B,正确的应为“?x∈R,均有x2+x+1≥0”;选项C,可由奇函数的性质说明正确;选项D,由三角函数的知识可得sinx+cosx的值域为[
说明错误;选项B,正确的应为“?x∈R,均有x2+x+1≥0”;选项C,可由奇函数的性质说明正确;选项D,由三角函数的知识可得sinx+cosx的值域为[ ,
, ],因为
],因为 ∉[
∉[ ,
, ],故错误.
],故错误.解答:选项A,当x=
 时,sin
时,sin =
= ,cos
,cos =
= ,显然有x∈(0,π),但sinx<cosx,故A错误;
,显然有x∈(0,π),但sinx<cosx,故A错误;选项B,命题“?x∈R使得x2+x+1<0”的否定应该为:“?x∈R,均有x2+x+1≥0”,故B错误;
选项C,当a=0时,数f(x)=x3+x显然为奇函数,当f(x)=x3+ax2+x为奇函数时,由f(0)=0可得a=0,
故“a=0”是“函数f(x)=x3+ax2+x为奇函数”的充要条件,故C正确;
选项D,sinx+cosx=
 sin(x+
sin(x+ )∈[
)∈[ ,
, ],因为
],因为 ∉[
∉[ ,
, ],
],故不存在x∈R,使
 ,故D错误.
,故D错误.故选C
点评:本题考查命题真假的判断,涉及函数的奇偶性和三角函数的性质以及特称命题的否定,属基础题.

练习册系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B. ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,乙比甲成绩稳定,应该选乙参加比赛
,乙比甲成绩稳定,应该选乙参加比赛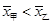 ,甲比乙成绩稳定,应该选甲参加比赛
,甲比乙成绩稳定,应该选甲参加比赛 :函数
:函数 (
( 且
且 )的图像恒过点
)的图像恒过点 ;
; :函数
:函数 有两个零点.
有两个零点.  为假命题 D.
为假命题 D. 为真命题
为真命题 的导函数
的导函数 的图象如上图所示,则下列说法正确的是 ( )
的图象如上图所示,则下列说法正确的是 ( ) 内单调递减 B、函数
内单调递减 B、函数 内单调递增
内单调递增 处取极大值 D、函数
处取极大值 D、函数 处取极小值
处取极小值