Question

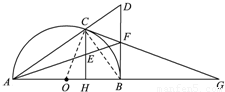
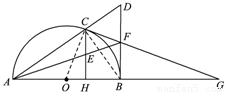
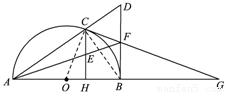
如图，已知C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G.

（1）求证：CG是⊙O的切线；

（2）若FB=FE=2，求⊙O的半径．

 

Answer 1

【答案】

(1)证明:如图，连接CB、OC.

 

∵AB是直径，∴∠ACB＝90°. ∵CH⊥AB，DB⊥AB，

∴△AEH∽△AFB，△ACE∽△ADF，

∴.

又∵HE＝EC，∴BF＝FD.

F是BD中点，。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分

∴∠BCF=∠CBF=90°-∠CBA

=∠CAB=∠ACO，

∴∠OCF=90°，∴CG是⊙O的切线 .。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。7分

(2)由FC=FB=FE，得∠FCE=∠FEC，

可证得FA＝FG，且AB＝BG.

由切割线定理，得

.①

在Rt△BGF中，由勾股定理，得

.②

由①②得-4FG-12=0，

解得FG＝6或FG＝-2（舍去）.

∴AB＝BG＝，∴⊙O半径为.。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分

【解析】略