题目内容
已知定义域为R的函数
是奇函数.
（1）求
；
（2）是否存在最大的常数k,对于任意
实数都有
,求出k.;若不存在，说明理由。
（3）若对任意的
，不等式
恒成立，求k的取值范围.
解 （1） 因为
是R上的奇函数，所以
从而有
又由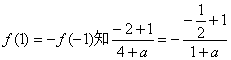
，解得
………………………………..4分
（2）由（1）知
由上式易知在R上为减函数，
，所以k=-1\2. …………………….4分
（3）解法一：由（1）知
由上式易知在R上为减函数，
又因是奇函数，从而不等式
等价于
因是R上的减函数，由上式推得
即对一切
从而
………………………………………….…………….5分
解法二：由（1）知
又由题设条件得
即
整理得
，因底数2>1，故
上式对一切
均成立，从而判别式
练习册系列答案
相关题目