题目内容
 设数列{an}的前项和为Sn,且Sn=
设数列{an}的前项和为Sn,且Sn= ,{bn}为等差数列,且a1=b1,a2(b2-b1)=a1.
,{bn}为等差数列,且a1=b1,a2(b2-b1)=a1.
(Ⅰ)求数列{an}和{bn}通项公式;
(Ⅱ)设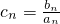 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
解:(Ⅰ)当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=( )-(
)-(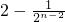 )=
)= ,
,
经验证当n=1时,此式也成立,所以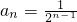 ,从而b1=a1=1,
,从而b1=a1=1, ,
,
又因为{bn}为等差数列,所以公差d=2,∴bn=1+(n-1)•2=2n-1,
故数列{an}和{bn}通项公式分别为: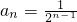 ,bn=2n-1.
,bn=2n-1.
(Ⅱ)由(Ⅰ)可知 ,
,
所以 +(2n-1)•2n-1 ①
+(2n-1)•2n-1 ①
①×2得 +(2n-3)•2n-1+(2n-1)•2n ②
+(2n-3)•2n-1+(2n-1)•2n ②
①-②得: -(2n-1)•2n
-(2n-1)•2n
= =1+2n+1-4-(2n-1)•2n=-3-(2n-3)•2n.
=1+2n+1-4-(2n-1)•2n=-3-(2n-3)•2n.
∴数列{cn}的前n项和 .
.
分析:(Ⅰ)由 可求数列{an}的通项公式,进而可求数列{bn}通项公式;
可求数列{an}的通项公式,进而可求数列{bn}通项公式;
(Ⅱ)由(Ⅰ)可知 ,故可用错位相减法来求数列的前n项和.
,故可用错位相减法来求数列的前n项和.
点评:本题为数列的求通项和求和的综合应用,涉及等差等比数列以及错位相减法求和,属中档题.
当n≥2时,an=Sn-Sn-1=(
 )-(
)-(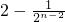 )=
)= ,
,经验证当n=1时,此式也成立,所以
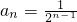 ,从而b1=a1=1,
,从而b1=a1=1, ,
,又因为{bn}为等差数列,所以公差d=2,∴bn=1+(n-1)•2=2n-1,
故数列{an}和{bn}通项公式分别为:
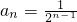 ,bn=2n-1.
,bn=2n-1.(Ⅱ)由(Ⅰ)可知
 ,
,所以
 +(2n-1)•2n-1 ①
+(2n-1)•2n-1 ①①×2得
 +(2n-3)•2n-1+(2n-1)•2n ②
+(2n-3)•2n-1+(2n-1)•2n ②①-②得:
 -(2n-1)•2n
-(2n-1)•2n=
 =1+2n+1-4-(2n-1)•2n=-3-(2n-3)•2n.
=1+2n+1-4-(2n-1)•2n=-3-(2n-3)•2n.∴数列{cn}的前n项和
 .
.分析:(Ⅰ)由
 可求数列{an}的通项公式,进而可求数列{bn}通项公式;
可求数列{an}的通项公式,进而可求数列{bn}通项公式;(Ⅱ)由(Ⅰ)可知
 ,故可用错位相减法来求数列的前n项和.
,故可用错位相减法来求数列的前n项和.点评:本题为数列的求通项和求和的综合应用,涉及等差等比数列以及错位相减法求和,属中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组