题目内容

设函数f(x)=|lgx|,若0＜a＜b,且f(a)＞f(b),证明ab＜1.

证法一:由已知，f(x)=|lgx|=其图象如下图.

∵0＜a＜b,f(a)＞f(b),

  

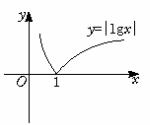
∴a、b不可能同时在区间［1,+∞)上.又由于0＜a＜b,故必有a∈(0,1).

①若b∈(0,1),显然有ab＜1；

②若b∈［1,+∞),

由f(a)＞f(b)有－lga＞lgb.

∴lg(ab)＜0,ab＜1.

综上，ab＜1成立.

证法二:∵f(a)＞f(b),∴|lga|＞|lgb|.

从而(lga)2＞(lgb)2,

(lga+lgb)(lga－lgb)＞0,

lg(ab)·lg＞0.

∵0＜a＜b,∴0＜＜1,lg＜0.

∴lg(ab)＜0,ab＜1.

练习册系列答案
相关题目
设函数f(x)=a(x+
1x
)+2lnx，g(x)=x2．
（I）若a＞0且a≠2，直线l与函数f（x）和函数g（x）的图象相切于一点，求切线l的方程．
（II）若f（x）在[2，4]内为单调函数，求实数a的取值范围．
（2012•朝阳区二模）设函数f(x)=alnx+
2
a
2
 
x
(a≠0)．
（1）已知曲线y=f（x）在点（1，f（1））处的切线l的斜率为2-3a，求实数a的值；
（2）讨论函数f（x）的单调性；
（3）在（1）的条件下，求证：对于定义域内的任意一个x，都有f（x）≥3-x．
（2011•顺义区二模）设函数f(x)=
ax
x2+b
(a＞0)．
（1）若函数f（x）在x=-1处取得极值-2，求a，b的值；
（2）若函数f（x）在区间（-1，1）内单调递增，求b的取值范围；
（3）在（1）的条件下，若P（x0，y0）为函数f(x)=
ax
x2+b
图象上任意一点，直线l与f（x）的图象切于点P，求直线l的斜率的取值范围．
（2012•太原模拟）设函数f(x)=a(x+
1
x
)+2lnx，g(x)=x2．
（1）若a=
1
2
时，直线l与函数f（x）和函数g（x）的图象相切于同一点，求切线l的方程；
（2）若f（x）在[2，4]内为单调函数，求实数a的取值范围．
说明：请考生在第22、23、24三题中任选一题作答，如果多做，则按所做第一题记分．
设函数f(x)=
3
2
-
3
sin2ωx-sinωxcosωx(ω＞0)，且y=f（x）的图象的一个对称中心到最近的对称轴的距离为
π
4

（l）求ω的值；
（2）将函数y=f（x）图象向左平移
π
3
个单位，得到函数y=g（x）的图象，求y=g（x）在区间[0，
π
2
]上的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网