题目内容
如图所示，已知O为平行四边形ABCD内一点，| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
| a |
| b |
| c |
分析：结合平行四边形ABCD的性质，由向量的加法及减法的三角形法则进行求解．
解答：解：由题意在平行四边形ABCD中：
∵
=
，
=
，
∴
=
-
=
-
，
∴
=
=
-
，
∴
=
+
=
-
+
，
故答案为：
-
+
．
∵
| OA |
| a |
| OB |
| b |
∴
| BA |
| OA |
| OB |
| a |
| b |
∴
| CD |
| BA |
| a |
| b |
∴
| OD |
| OC |
| CD |
| a |
| b |
| c |
故答案为：
| a |
| b |
| c |
点评：本题考查两个向量的加减法的法则及几何意义，主要利用三角形法则进行求解，考查了数形结合思想．
练习册系列答案
相关题目
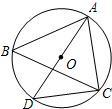
如图所示，已知⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若AD=3，AC=2，则cosD的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
A：如图所示，已知AB为⊙O的直径，AC为弦，OD∥BC，交AC于点D，BC=4cm，
（2013•潮州二模）如图所示，已知AB为圆O的直径，点D为线段AB上一点，且AD=
=
，
=
，
=
，则
=______