题目内容
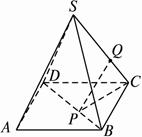
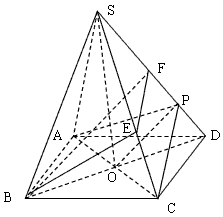
如图,正四棱锥S-ABCD 的底面是边长为a的正方形,O为底面对角线交点,侧棱长是底面边长的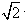 倍,P为侧棱SD上的点,
倍,P为侧棱SD上的点,
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,F为SD中点,求证:BF∥平面PAC;
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
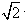 倍,P为侧棱SD上的点,
倍,P为侧棱SD上的点, (Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,F为SD中点,求证:BF∥平面PAC;
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
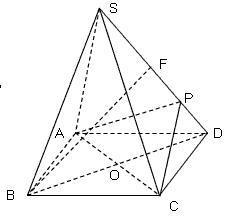
| 解:(Ⅰ)连接SO, ∵四边形ABCD为正方形, ∴AC⊥BD且O为AC的中点, 又∵SA=SC, ∴SO⊥AC, 又  , ,∴AC⊥平面SBD, 又 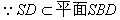 , ,∴AC⊥SD。 (Ⅱ)连接OP, 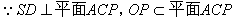 , ,∴OP⊥SD, 又△SBD中, 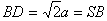 ,且F为SD中点, ,且F为SD中点, ∴BF⊥SD, 因为 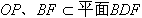 , ,所以OP∥BF, 又 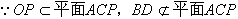 , ,∴BF∥平面PAC。 (Ⅲ)解:存在E,使得BE∥平面PAC; 过F作FE∥PC交PC于E,连接BE,则E为所要求点, ∵FE∥PC, 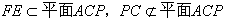 , ,∴FE∥平面PAC, 由(Ⅱ)知:BF∥平面PAC,而FE∩BF=F, ∴平面BEF∥平面PAC, ∴BE∥平面PAC, ∵OP∥BF,O为BD的中点, ∴P为FD的中点, 又因为F为SD的中点, ∴ 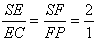 , ,所以,在侧棱SC上存在点E, 当SE:EC=2:1时,BE∥平面PAC。 |
 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°. 12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )
12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )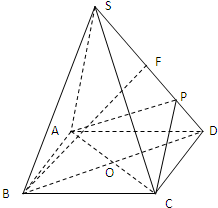 如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的
如图,正四棱锥S-ABCD 的底面是边长为a正方形,O为底面对角线交点,侧棱长是底面边长的 (2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的
(2006•西城区二模)如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的