题目内容
【题目】设数列![]() 的各项都是正数,若对于任意的正整数
的各项都是正数,若对于任意的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,则称函数
成等比数列,则称函数![]() 为“
为“![]() 型”数列.
型”数列.
(1)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”数列,又是“
型”数列,又是“![]() 型”数列,求证:数列
型”数列,求证:数列![]() 是等比数列.
是等比数列.
【答案】(1)2;(2) 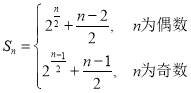 (3)见证明
(3)见证明
【解析】
(1)根据已知![]() 是“
是“![]() 型”数列,即
型”数列,即![]() 成等比数列,那么可知
成等比数列,那么可知![]() 是等比数列,由条件可直接求出
是等比数列,由条件可直接求出![]() ,进而得
,进而得![]() 的值;(2)当n为奇数时
的值;(2)当n为奇数时![]() ,当n为偶数时,根据已知可计算出
,当n为偶数时,根据已知可计算出![]() ,由此得到
,由此得到![]() ;(3)先写出
;(3)先写出![]() 时的“
时的“![]() 型”数列和“
型”数列和“![]() 型”数列,公比分别为
型”数列,公比分别为![]() 和
和![]() ,再写出
,再写出![]() 和
和![]() 时的“
时的“![]() 型”数列,公比分别为
型”数列,公比分别为![]() 和
和![]() ,根据数列中的公共项可得公比之间的关系
,根据数列中的公共项可得公比之间的关系![]() ,再由
,再由![]() 时的3个“
时的3个“![]() 型”数列的通项公式,可推得
型”数列的通项公式,可推得![]() 是等比数列。
是等比数列。
解:(1)由![]() 是“
是“![]() ”数列,所以
”数列,所以![]() 成等比,所以
成等比,所以![]() 成等比数列,且公比
成等比数列,且公比![]() ,
,
则![]()
(2)由![]() 是“
是“![]() ”数列,所以
”数列,所以![]() 成等比,所以当
成等比,所以当![]() 为奇数时:
为奇数时:![]() ;
;
由![]() 是“
是“![]() ”数列,所以
”数列,所以![]() 成等比,所以当
成等比,所以当![]() 为偶数时:
为偶数时:![]() ;
;
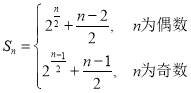
(3)由![]() 是“
是“![]() ”数列,所以
”数列,所以![]() 成等比,
成等比,
设其公比为![]() ,又
,又![]() 是“
是“![]() ”数列,则
”数列,则![]() 成等比数列,设其公比为
成等比数列,设其公比为![]() ,同理,设
,同理,设![]() 的公比为
的公比为![]() ,
,![]() 的公比为
的公比为![]() (
(![]() 。
。
那么![]() ,所以
,所以![]() 。
。
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 。
。
综上得:![]() ,
,![]() ,所以
,所以![]() 是等比数列
是等比数列

练习册系列答案
相关题目