题目内容
（ ）
A． >0 | B．>－3 | C．<1 | D． |
D
解析试题分析：方法一：由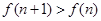
，可得
,化简得
,要使对于任意正整数n都成立，则
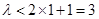，即
.
方法二：因
,则
在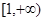
上为单调递增函数，但考虑到
为二次函数，且单调性只需满足整数点，所以二次函数的对称轴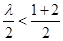
（满足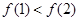
，而不是对称轴
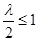），解得.
考点：函数的恒成立问题（一般采用分离常数法）.
练习册系列答案
相关题目
，判断函数在定义域内的单调性
内存在极值，求实数m的取值范围。函数
的定义域为（ ）
A． | B． | C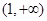． | D． |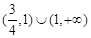
已知集合
，
，则
（ ）
A． | B．(1，3) | C．(1， ) | D．(3，) |
，
的图象可能是下列图象中的( )
设二次函数
在区间[0,1]上单调递减，且
，则实数
的取值范围是( )．
| A．(－∞，0] | B．[2，＋∞) | C．[0,2] | D．(－∞，0]∪[2，＋∞) |
已知实数
满足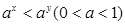
，则下列关系式恒成立的是（ ）
A． | B． |
C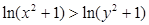． | D． |
设a＝40.8，b＝80.46，c＝(
)－1.2，则a，b，c的大小关系为( )
| A．a>b>c | B．b>a>c | C．c>a>b | D．c>b>a |