题目内容
函数f(x)=
(ax+a-x),(a>0且a≠1).
(1)讨论f(x)的奇偶性;
(2)若函数f(x)的图象经过点(2,
),求f(x).
| 1 |
| 2 |
(1)讨论f(x)的奇偶性;
(2)若函数f(x)的图象经过点(2,
| 41 |
| 9 |
(1)函数定义域为R,
∵f(x)=
(ax+a-x),(a>0且a≠1).
∴f(-x)=
(ax+a-x)=f(x),
∴f(x)是偶函数.
(2)∵f(x)的图象过点(2,
)
∴
(a2+a-2)=
,
即9a4-82a2+9=0,
解得a2=9或a2=
∵a>0且a≠1,
∴a=3或a=
.
即f(x)=
(3x+3-x).
∵f(x)=
| 1 |
| 2 |
∴f(-x)=
| 1 |
| 2 |
∴f(x)是偶函数.
(2)∵f(x)的图象过点(2,
| 41 |
| 9 |
∴
| 1 |
| 2 |
| 41 |
| 9 |
即9a4-82a2+9=0,
解得a2=9或a2=
| 1 |
| 9 |
∵a>0且a≠1,
∴a=3或a=
| 1 |
| 3 |
即f(x)=
| 1 |
| 2 |

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
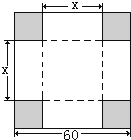


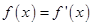 的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)=
的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)=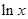 ,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )
,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )



 的定义域是 .
的定义域是 .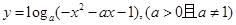 有最小值,则实数
有最小值,则实数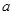 的取值范围是
的取值范围是