Question

（本小题满分14分）

已知函数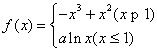

（Ⅰ）求f(x)在［-1，e］（e为自然对数的底数）上的最大值；

（Ⅱ）对任意给定的正实数a，曲线y= f(x)上是否存在两点P，Q，使得△POQ是以O为直角顶点的直角三角形，且此三角形斜边中点在y轴上？

Answer 1

解：（Ⅰ）因为f(x)=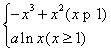

当-1≤x＜1时，f ′(x)=- x (3x -2)，

解f ′(x)＞0得0＜x＜：解f ′(x) ＜0得-1＜x＜0或＜x＜1

∴f(x)在（-1，0）和（，1）上单减，在（0，）上单增，

从而f (x)在x=处取得极大值f ()=…………………………………………………（3分）

又∵f(-1)=2，f(1)=0，

∴f(x)在［-1，1)上的最大值为2. …………………………………………………………（4分）

当1≤x≤e时，f(x)=alnx，

当a≤0时，f(x)≤0；

当a＞0时，f(x)在［1，e］单调递增；

∴f(x)在［1，e］上的最大值为a. ……………………………………………………………（6分）

∴当a≥2时，f(x)在［-1，e］上的最大值为a；

当a＜2时，f(x)在［-1，e］上的最大值为2. ………………………………………………（8分）

（Ⅱ）假设曲线y= f(x)上存在两点P，Q满足题意，则P，Q只能在y轴两侧，不妨设P（t, f(t)）(t＞0),则Q（-t，t³+t²），且t≠1………………………………………………………………（9分）

∵△POQ是以O为直角顶点的直角三角形

∴=0，即- t²+f(t)（t³+t²）=0（*）…………………………………………………（10分）

是否存在P，Q等价于方程（*）是否有解.

若0＜t＜1，则f(x)=- t³+t²，代入方程（*）得：- t²+（-t³+t²）（t³+t²）=0，

即：t⁴-t²+1=0，而此方程无实数解，………………………………………………………（11分）

②当t＞1时，

∴f(t)=alnt，代入方程（*）得：- t²+ alnt·（t³+t²）=0，

即：……………………………………………………………………………（12分）

设h(x)=(x+1)lnx(x≥1),则h′(x)=lnx++1＞0在［1,+∞)恒成立.

∴h(x)在［1,+∞)上单调递增，从而h(x)≥h(1)=0，则h(x)的值域为［0,+∞).

∴当a＞0时，方程=（t+1）lnt有解，即方程（*）有解. ……………………………（13分）

∴对任意给定的正实数a，曲线y=f(x)上总存在两点P，Q，使得△POQ是以O为直角顶点的直角三角形，且此三角形斜边中点在y轴上. ………………………………………………（14分）