题目内容
在平面直角坐标系xOy中,动点M到直线x=-1的距离等于它到圆F:(x-2)2+y2=1的点的最小距离.
(1)求点M的轨迹方程;
(2)已知过点F的直线与点M的轨迹交于A,B两点,且|AF|=8,求|BF|的长.
(1)求点M的轨迹方程;
(2)已知过点F的直线与点M的轨迹交于A,B两点,且|AF|=8,求|BF|的长.
分析:(1)利用动点M到直线x=-1的距离等于它到圆F:(x-2)2+y2=1的点的最小距离,建立方程,化简可得点M的轨迹方程;
(2)确定AB的方程,求出A,B的坐标,利用抛物线的定义,即可求得|BF|的长.
(2)确定AB的方程,求出A,B的坐标,利用抛物线的定义,即可求得|BF|的长.
解答:解:(1)设动点M(x,y),则
∵动点M到直线x=-1的距离等于它到圆F:(x-2)2+y2=1的点的最小距离
∴|x+1|=
,…(3分)
化简得:6x-2+2|x+1|=y2,
当x≥-1时,y2=8x; …(5分)
当x<-1时,y2=4x-4<-8,不合题意.
所以点M的轨迹方程为:y2=8x.…(7分)
(2)抛物线的准线方程为x=-2.
过点A作准线的垂线AM,垂足为M,AM交y轴于点E,过点A作x轴垂线,垂足为H.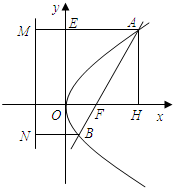
过点B作准线的垂线BN,垂足为N,
由抛物线的定义知:AF=AM=8.
因为ME=OF=2,所以AE=6,FH=4.
在Rt△AHF中,AF=8,FH=4,所以∠AFH=60°.…(10分)
直线AB的方程为y=
(x-2)代入y2=8x,可得
3x2-20x+12=0
∴x=6,或x=
∴A(6,4
),B(
,-
).
∴BF=BN=
+2=
. …(14分)
∵动点M到直线x=-1的距离等于它到圆F:(x-2)2+y2=1的点的最小距离
∴|x+1|=
| (x-2)2+(y-0)2-1 |
化简得:6x-2+2|x+1|=y2,
当x≥-1时,y2=8x; …(5分)
当x<-1时,y2=4x-4<-8,不合题意.
所以点M的轨迹方程为:y2=8x.…(7分)
(2)抛物线的准线方程为x=-2.
过点A作准线的垂线AM,垂足为M,AM交y轴于点E,过点A作x轴垂线,垂足为H.

过点B作准线的垂线BN,垂足为N,
由抛物线的定义知:AF=AM=8.
因为ME=OF=2,所以AE=6,FH=4.
在Rt△AHF中,AF=8,FH=4,所以∠AFH=60°.…(10分)
直线AB的方程为y=
| 3 |
3x2-20x+12=0
∴x=6,或x=
| 2 |
| 3 |
∴A(6,4
| 3 |
| 2 |
| 3 |
4
| ||
| 3 |
∴BF=BN=
| 2 |
| 3 |
| 8 |
| 3 |
点评:本题考查轨迹方程,考查抛物线的定义,考查学生的计算能力,确定抛物线的方程是关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是