题目内容
下列命题是真命题的有 ( )
①“等边三角形的三个内角均为60°”的逆命题;
②“若k>0,则方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题.
| A.0个 | B.1个 | C.2个 | D.3个 |
C
解析试题分析:对于命题①,其逆命题为:三个内角均为 的三角形为等边三角形,显然是真命题;对于命题②,当
的三角形为等边三角形,显然是真命题;对于命题②,当 时,
时, ,所以原命题是真命题,因为原命题和其逆否命题真假性相同,所以其逆否命题是真命题;对于命题③,其否命题是:不全等的三角形面积不相等,两个三角形即使不全等,其面积有可能相等,所以是假命题.真命题有①②,共有两个,故选C.
,所以原命题是真命题,因为原命题和其逆否命题真假性相同,所以其逆否命题是真命题;对于命题③,其否命题是:不全等的三角形面积不相等,两个三角形即使不全等,其面积有可能相等,所以是假命题.真命题有①②,共有两个,故选C.
考点:本题考查的知识点是四种命题的关系,及其真假性的关系,正确把握四种命题真假性的关系以及判断命题的真假性是解题的关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
设 ,且
,且 ,则“函数
,则“函数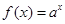 ”在R上是增函数”是“函数
”在R上是增函数”是“函数 ”在R上是增函数”的( )
”在R上是增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题
 ;命题
;命题 关于
关于 的方程
的方程 有实数解,则
有实数解,则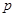 是
是 的( ).
的( ).
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
对于常数 、
、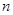 ,“
,“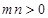 ”是“方程
”是“方程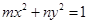 的曲线是椭圆”的( )
的曲线是椭圆”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
等比数列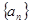 中,
中, ,则“
,则“ ”是“
”是“ ” 的( )
” 的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
以下判断正确的是 ( )
| A.命题“负数的平方是正数”不是全称命题 |
B.命题“ ”的否定是“ ”的否定是“ ” ” |
C.“ ”是“函数 ”是“函数 的最小正周期是 的最小正周期是 ”的必要不充分条件 ”的必要不充分条件 |
D.“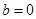 ”是“函数 ”是“函数 是偶函数”的充要条件 是偶函数”的充要条件 |
已知 ,
, ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
购物大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的( )
| A.充分条件 | B.必要条件 |
| C.充分必要条件 | D.既非充分也非必要条件 |
 为三角形的内角,则
为三角形的内角,则 的 ( )
的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |