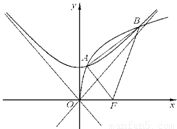
题目内容
设 是以
是以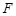 为焦点的抛物线
为焦点的抛物线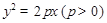 ,
,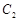 是以直线
是以直线 与
与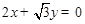 为渐近线,以
为渐近线,以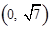 为一个焦点的双曲线.
为一个焦点的双曲线.
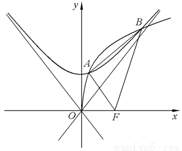
(1)求双曲线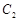 的标准方程;
的标准方程;
(2)若 与
与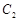 在第一象限内有两个公共点
在第一象限内有两个公共点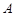 和
和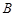 ,求
,求 的取值范围,并求
的取值范围,并求 的最大值;
的最大值;
(3)若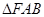 的面积
的面积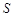 满足
满足 ,求
,求 的值.
的值.
【答案】
(1) (2)当且仅当
(2)当且仅当 时
时 的最大值为9
的最大值为9
(3)
【解析】本试题主要考查了双曲线方程的求解以及双曲线的性质,和直线与双曲线的位置关系的综合运用。
(1)利用双曲线的性质得到关于a,b,c的关系式得到方程的求解。
(2)联立方程组抛物线于双曲线的方程,和韦达定理,以及向量的关系式化简得到最值
(3)利用面积的公式,底乘以高的一半,以及运用向量的数量积表示面积公式得到P的值解:

(1)设双曲线 的标准方程为:
的标准方程为: 则据题得:
则据题得:
又

 双曲线
双曲线 的标准方程为:
的标准方程为:
(2)将 代入到
代入到 中并整理得:
中并整理得:
设 则
则
 又
又



 当且仅当
当且仅当 时
时 的最大值为9
的最大值为9
(3)直线 的方程为:
的方程为: 即
即
 到直线
到直线 的距离为:
的距离为:



又



练习册系列答案
相关题目
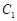 是以
是以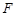 为焦点的抛物线
为焦点的抛物线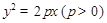 ,
, 是以直线
是以直线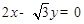 与
与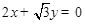 为渐近线,以
为渐近线,以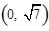 为一个焦点的双曲线.
为一个焦点的双曲线. 和
和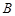 ,求
,求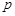 的取值范围,并求
的取值范围,并求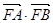 的最大值;
的最大值;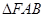 的面积
的面积 满足
满足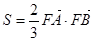 ,求
,求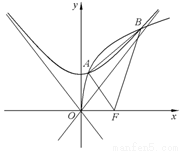
 的左,右焦点为
的左,右焦点为 ,
, ,(1,
,(1, )为椭圆上一点,椭圆的
)为椭圆上一点,椭圆的 轴的对称点记为M,设
轴的对称点记为M,设 .
. ;
; 求|PQ|的取值范围
求|PQ|的取值范围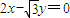 与
与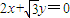 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.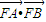 的最大值;
的最大值; 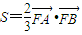 ,求p的值.
,求p的值.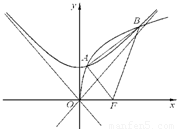
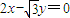 与
与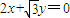 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线. 的最大值;
的最大值; 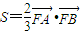 ,求p的值.
,求p的值.