题目内容
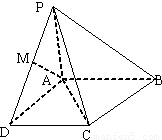
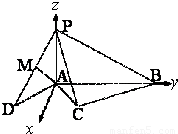
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,PA=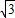 ,∠ACB=90°,M是线段PD上的一点(不包括端点).
,∠ACB=90°,M是线段PD上的一点(不包括端点).(Ⅰ)求证:BC⊥平面PAC;
(Ⅱ)求二面角D-PC-A的正切值;
(Ⅲ)试确定点M的位置,使直线MA与平面PCD所成角θ的正弦值为
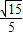 .
.
【答案】分析:(Ⅰ)由PA⊥底面ABCD,BC?平面AC,知PA⊥BC,由∠ACB=90°,知BC⊥AC,由此能够证明BC⊥平面PAC.
(Ⅱ)取CD的中点E,则AE⊥CD,故AE⊥AB,由PA⊥底面ABCD,知PA⊥AE,建立空间直角坐标系,利用向量法能求出二面角D-PC-A的正切值.
(Ⅲ)设M(x,y,z),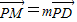 ,则(x,y,z-
,则(x,y,z-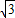 )=m(
)=m(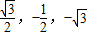 ),解得点M(
),解得点M(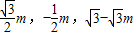 ),由此能够推导出当M为PD的中点时,直线AM与平面PCD所成角的正弦值为
),由此能够推导出当M为PD的中点时,直线AM与平面PCD所成角的正弦值为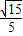 .
.
解答:解:(Ⅰ)∵PA⊥底面ABCD,BC?平面AC,∴PA⊥BC,
∵∠ACB=90°,
∴BC⊥AC,又PA∩AC=A,
∴BC⊥平面PAC.
(Ⅱ)取CD的中点E,则AE⊥CD,
∴AE⊥AB,又PA⊥底面ABCD,∴PA⊥AE,
建立如图所示空间直角坐标系,
则A(0,,0,0),P(0,0,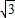 ),C(
),C(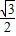 ,
, ,0),D(
,0),D(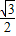 ,-
,- ,0)
,0)
∴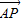 =(0,0,
=(0,0,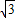 ),
),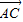 =(
=(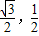 ,0),
,0),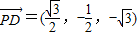 ,
,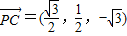 ,
,
设平面PAC的一个法向量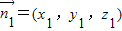 ,则
,则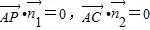 ,
,
∴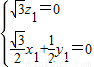 ,∴
,∴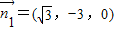 .
.
设平面PDC的一个法向量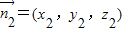 ,则
,则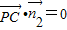 ,
,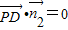 ,
,
∴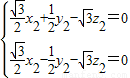 ,∴
,∴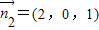 ,
,
设二面角D-PC-A的平面角为θ,
∴cosθ=|cos<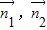 >|=|
>|=|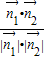 |=|
|=|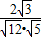 |=
|=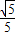 ,
,
故二面角D-PC-A的正切值为2.
(Ⅲ)设M(x,y,z),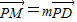 ,
,
则(x,y,z-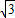 )=m(
)=m(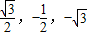 ),
),
解得点M(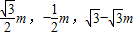 ),即
),即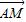 =(
=(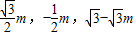 ),
),
由sinθ=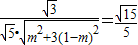 ,得m=1(不合题意舍去)或m=
,得m=1(不合题意舍去)或m= ,
,
所以当M为PD的中点时,直线AM与平面PCD所成角的正弦值为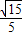 .
.
点评:本题考查直线与平面垂直的证明,考查二面角的正切值的求法,考查满足条件的点的位置的探索.解题时要认真审题,仔细解答,注意等价转化思想和向量法的合理运用.
(Ⅱ)取CD的中点E,则AE⊥CD,故AE⊥AB,由PA⊥底面ABCD,知PA⊥AE,建立空间直角坐标系,利用向量法能求出二面角D-PC-A的正切值.
(Ⅲ)设M(x,y,z),
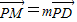 ,则(x,y,z-
,则(x,y,z-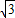 )=m(
)=m(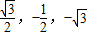 ),解得点M(
),解得点M(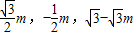 ),由此能够推导出当M为PD的中点时,直线AM与平面PCD所成角的正弦值为
),由此能够推导出当M为PD的中点时,直线AM与平面PCD所成角的正弦值为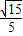 .
.解答:解:(Ⅰ)∵PA⊥底面ABCD,BC?平面AC,∴PA⊥BC,
∵∠ACB=90°,
∴BC⊥AC,又PA∩AC=A,
∴BC⊥平面PAC.
(Ⅱ)取CD的中点E,则AE⊥CD,
∴AE⊥AB,又PA⊥底面ABCD,∴PA⊥AE,
建立如图所示空间直角坐标系,
则A(0,,0,0),P(0,0,
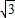 ),C(
),C(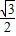 ,
, ,0),D(
,0),D(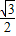 ,-
,- ,0)
,0)
∴
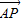 =(0,0,
=(0,0,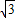 ),
),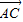 =(
=(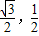 ,0),
,0),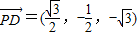 ,
,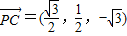 ,
,设平面PAC的一个法向量
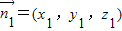 ,则
,则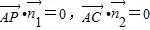 ,
,∴
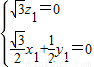 ,∴
,∴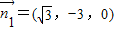 .
.设平面PDC的一个法向量
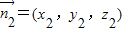 ,则
,则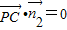 ,
,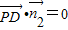 ,
,∴
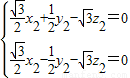 ,∴
,∴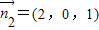 ,
,设二面角D-PC-A的平面角为θ,
∴cosθ=|cos<
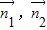 >|=|
>|=|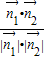 |=|
|=|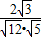 |=
|=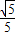 ,
,故二面角D-PC-A的正切值为2.
(Ⅲ)设M(x,y,z),
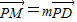 ,
,则(x,y,z-
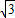 )=m(
)=m(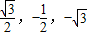 ),
),解得点M(
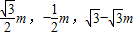 ),即
),即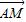 =(
=(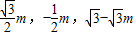 ),
),由sinθ=
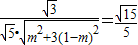 ,得m=1(不合题意舍去)或m=
,得m=1(不合题意舍去)或m= ,
,所以当M为PD的中点时,直线AM与平面PCD所成角的正弦值为
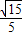 .
.点评:本题考查直线与平面垂直的证明,考查二面角的正切值的求法,考查满足条件的点的位置的探索.解题时要认真审题,仔细解答,注意等价转化思想和向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=