题目内容
已知直线y=-4上有一动点Q,过点Q作垂直于x轴的直线l1,动点P在直线l1上,若点P满足OP⊥OQ(O为坐标原点 ),记点 P的轨迹为C
(1)求曲线C的方程
(2)过点A(-4,0)作直线l2与曲线C交于M,N两点,若与y轴交于点R,且
+
=
,求直线l2的方程.
(1)求曲线C的方程
(2)过点A(-4,0)作直线l2与曲线C交于M,N两点,若与y轴交于点R,且
| 1 |
| |AM| |
| 1 |
| |AN| |
| 3 |
| |AR| |
分析:(1)设P(x,y),可得Q(x,-4),根据垂直直线的斜率之积为-1,利用直线的斜率公式列式,化简即可得到曲线C的方程;
(2)设直线l2方程为y=k(x+4),与抛物线消去x得
y2-(
+4)y+16=0.设M(x1,y1),N(x2,y2),由韦达定理得到y1+y2=4k2+8k,y1y2=16k2.然后将
+
=
转化为关于y1、y2和k的等式,代入前面证出的关系式化简得到关于k的方程,解出k值即可得到直线l2的方程.
(2)设直线l2方程为y=k(x+4),与抛物线消去x得
| 1 |
| k2 |
| 8 |
| k |
| 1 |
| |AM| |
| 1 |
| |AN| |
| 3 |
| |AR| |
解答:解:(1)设点P的坐标为(x,y),则点Q的坐标为(x,-4).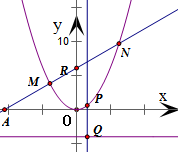
∵OP⊥OQ,∴kOP•kOQ=-1.
当x≠0时,得
•
=-1,化简得x2=4y.
当x=0时,P、O、Q三点共线,不符合题意,故x≠0.
综上所述,曲线C的方程为x2=4y(x≠0);
(2)设直线l2的方程为y=k(x+4),(k>0)
由
消去x,得
y2-(
+4)y+16=0.
设M(x1,y1),N(x2,y2),则y1+y2=4k2+8k,y1y2=16k2.
设直线l2的倾斜角为α,则|AM|=
,|AN|=
,|AR|=
=
∵
+
=
,∴
+
=
,
化简得
=
,即
=
,解之得k=1,
因此,直线l2的方程为y=x+4.

∵OP⊥OQ,∴kOP•kOQ=-1.
当x≠0时,得
| y |
| x |
| -4 |
| x |
当x=0时,P、O、Q三点共线,不符合题意,故x≠0.
综上所述,曲线C的方程为x2=4y(x≠0);
(2)设直线l2的方程为y=k(x+4),(k>0)
由
|
| 1 |
| k2 |
| 8 |
| k |
设M(x1,y1),N(x2,y2),则y1+y2=4k2+8k,y1y2=16k2.
设直线l2的倾斜角为α,则|AM|=
| y1 |
| sinα |
| y2 |
| sinα |
| |OR| |
| sinα |
| 4k |
| sinα |
∵
| 1 |
| |AM| |
| 1 |
| |AN| |
| 3 |
| |AR| |
| 1 | ||
|
| 1 | ||
|
| 3 | ||
|
化简得
| y1+y2 |
| y1y2 |
| 3 |
| 4k |
| 4k2+8k |
| 16k2 |
| 3 |
| 4k |
因此,直线l2的方程为y=x+4.
点评:本题给出动点满足的条件,求轨迹方程并求满足特殊条件的直线方程.着重考查了直线的基本量与基本形式、抛物线的简单几何性质和直线与圆锥曲线的位置关系等知识,属于中档题.

练习册系列答案
相关题目