题目内容
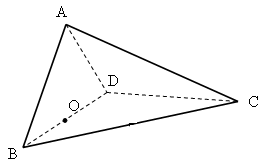
如图,四面体ABCD中,点O是BD的中点,且CA=CB=CD=BD=2,AB=AD=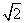 ,
,
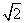 ,
,
(1)求证:平面ABD⊥平面BCD;
(2)求异面直线AB与CD所成角的余弦值。
(2)求异面直线AB与CD所成角的余弦值。
(1)证明:连结AO,
∵O为BD的中点,AB=AD,
∴AO⊥BD,BC=CD,
∴BD⊥CO,
∴ ,
,
在△AOC中,由已知可得AO=1, ,AC=2,
,AC=2,
∴∠AOC=90°,
即AO⊥OC,
又AO⊥BD,BD∩OC=O,
∴AO⊥平面BCD,
又∵AO 平面ABD,
平面ABD,
∴平面ABD⊥平面BCD。
(2)解:取AC的中点M,BC的中点E,连接ME,OE,OM,
则ME∥AB,OE∥DC,
∴∠OEM(或其补角)为异面直线AB与CD所成的角,
在△OME中, ,
,
∵OM是Rt△AOC斜边AC上的中线,
∴
∴
∴异面直线AB与CD所成角的余弦值为 。
。
∵O为BD的中点,AB=AD,
∴AO⊥BD,BC=CD,
∴BD⊥CO,
∴
 ,
,在△AOC中,由已知可得AO=1,
 ,AC=2,
,AC=2, ∴∠AOC=90°,
即AO⊥OC,
又AO⊥BD,BD∩OC=O,
∴AO⊥平面BCD,
又∵AO
 平面ABD,
平面ABD,∴平面ABD⊥平面BCD。
(2)解:取AC的中点M,BC的中点E,连接ME,OE,OM,
则ME∥AB,OE∥DC,
∴∠OEM(或其补角)为异面直线AB与CD所成的角,
在△OME中,
 ,
,∵OM是Rt△AOC斜边AC上的中线,
∴

∴

∴异面直线AB与CD所成角的余弦值为
 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
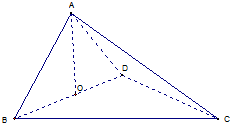 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.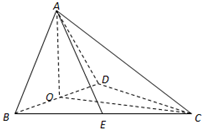 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.