题目内容
某电视台综艺频道组织的闯关游戏，游戏规定前两关至少过一关才有资格闯第三关，闯关者闯第一关成功得3分，闯第二关成功得3分，闯第三关成功得4分．现有一位参加游戏者单独面第一关、第二关、第三关成功的概率分别为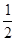
，
，
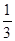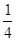，记该参加者闯三关所得总分为ζ．
(1)求该参加者有资格闯第三关的概率；
(2)求ζ的分布列和数学期望．
（1）
（2）
的分布列为
所以
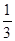
的数学期望
解析试题分析：解： ⑴设该参加者单独闯第一关、第二关、第三关成功的概率分别为
，
，
，该参加者有资格闯第三关为事件
．
则
． 4分
(2)由题意可知，的可能取值为
，，，，，
， 
，
，
，
，
所以的分布列为
8分
所以的数学期望
10分
考点：独立事件和互斥事件的概率
点评：主要是考查了分布列的求解以及互斥事件和独立事件的概率的运用，属于中档题。
练习册系列答案
阅读快车系列答案
相关题目
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：
性别与看营养说明列联表 单位: 名
| | 男 | 女 | 总计 |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
（2）根据以上列联表，能否在犯错误的概率不超过0.01的前提下认为性别与是否看营养说明之间有关系？
下面的临界值表供参考：
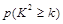 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
，其中
)
“肇实，正名芡实，因肇庆所产之芡实颗粒大、药力强，故名。”某科研所为进一步改良肇实，为此对肇实的两个品种（分别称为品种A和品种B）进行试验．选取两大片水塘，每大片水塘分成n小片水塘，在总共2n小片水塘中，随机选n小片水塘种植品种A，另外n小片水塘种植B．
（1）假设n=4，在第一大片水塘中，种植品种A的小片水塘的数目记为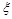
，求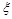的分布列和数学期望；
（2）试验时每大片水塘分成8小片，即n=8，试验结束后得到品种A和品种B在每个小片水塘上的每亩产量（单位：kg/亩）如下表：
| 号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 品种A | 101 | 97 | 92 | 103 | 91 | 100 | 110 | 106 |
| 品种B | 115 | 107 | 112 | 108 | 111 | 120 | 110 | 113 |
的一元二次方程
……
，解决下列两个问题：
是从
三个数中任取的一个数，
是从
三个数中任取的一个数，求方程
任取的一个数，
任取的一个数，求方程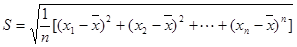
为摸出两球中白球的个数，
，且他们是否译出密码互不影响。
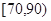段的有多少人；