题目内容
已知直线: (
( 为给定的正常数,
为给定的正常数, 为参数,
为参数, )构成的集合为
)构成的集合为 ,给出下列命题:
,给出下列命题:
①当 时,
时, 中直线的斜率为
中直线的斜率为 ;
;
② 中所有直线均经过一个定点;
中所有直线均经过一个定点;
③当 时,存在某个定点,该定点到
时,存在某个定点,该定点到 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当 时,
时, 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为 ;
;
⑤ 中的所有直线可覆盖整个平面.
中的所有直线可覆盖整个平面.
其中正确的是 (写出所有正确命题的编号).
【答案】
③④.
【解析】
试题分析: 既满足直线
既满足直线 的方程,也满足椭圆
的方程,也满足椭圆 的方程,且把直线
的方程,且把直线 的方程代入椭圆
的方程代入椭圆 的方程可得
的方程可得 直线
直线 为椭圆
为椭圆 的切线.①当
的切线.①当 时,
时, ①错;②
①错;② 为椭圆切线不经过定点,②错;③当
为椭圆切线不经过定点,②错;③当 时,点
时,点 在圆
在圆 上,圆心到圆上的距离相等,∴③正确;④当
上,圆心到圆上的距离相等,∴③正确;④当 时,
时, 为椭圆切线,当
为椭圆切线,当 中两直线分别与椭圆相切于的短轴两端点时,它们间的距离为
中两直线分别与椭圆相切于的短轴两端点时,它们间的距离为 ,∴④正确;⑤
,∴④正确;⑤ 为椭圆切线,不可覆盖整个平面.综上所述:③④正确.
为椭圆切线,不可覆盖整个平面.综上所述:③④正确.
考点:1.椭圆的几何性质;2.直线和椭圆的位置关系.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
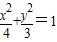 的左右顶点,F为椭圆的右焦点,P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
的左右顶点,F为椭圆的右焦点,P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.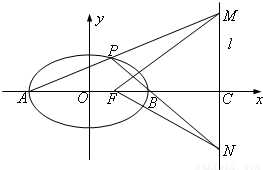
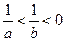 ,则
,则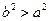 ;
;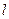 ,平面
,平面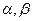 为不重合的两个平面.若
为不重合的两个平面.若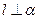 ,且
,且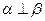 ,则
,则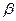 ;
;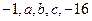 成等比数列,则
成等比数列,则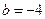 ;
;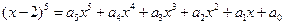 ,则
,则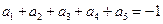 .
. .(写出所有真命题的序号)
.(写出所有真命题的序号)