题目内容
(本小题满分12分)
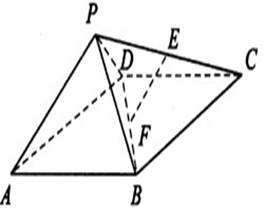
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点,
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求锐二面角B—PD—C的余弦值.
(1)如图,连接AC,
∵ABCD为矩形且F是BD的中点,
∴AC必经过F 1分
又E是PC的中点,
所以,EF∥AP 2分
∵EF在面PAD外,PA在面内,∴EF∥面PAD 4分
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD 面ABCD=AD,∴CD⊥面PAD,
面ABCD=AD,∴CD⊥面PAD,
又AP 面PAD,∴AP⊥CD 6分
面PAD,∴AP⊥CD 6分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD 7分
又AD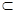 面PAD,所以,面PDC⊥面PAD 8分
面PAD,所以,面PDC⊥面PAD 8分
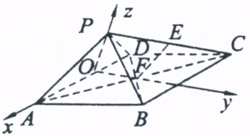
(3)由P作PO⊥AD于O,以OA为x轴,以OF为y轴,以OP为z轴,则
A(1,0,0),P(0,0,1) 9分
由(2)知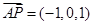 是面PCD的法向量,B(1,1,0),D(一1,0,0),
是面PCD的法向量,B(1,1,0),D(一1,0,0),
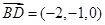 ,
,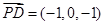 10分
10分
设面BPD的法向量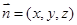 ,
,
由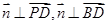 得
得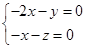
取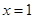 ,则
,则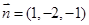 ,
,
向量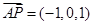 和
和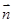 的夹角的余弦
的夹角的余弦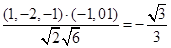 11分
11分
所以,锐二面角B—PD—C的余弦值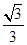 12分
12分
【解析】略

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案