题目内容
设奇函数f（x）的定义域为[-5，5]，在（0，5]上是减函数，又f（-3）=0，则不等式 xf（x）＜0的解集是
[-5，-3）∪（3，5]
[-5，-3）∪（3，5]
．分析：由题意可得，函数的图象关于原点对称，在[-5，0）上是增函数，且f（3）=0，画出函数f（x）的单调性示意图，由不等式 xf（x）＜0可得，x与f（x）
的符号相反，数形结合可得不等式的解集．
的符号相反，数形结合可得不等式的解集．
解答：
解：由题意可得，函数的图象关于原点对称，在[-5，0）上是增函数，且f（3）=0，
画出函数f（x）的单调性示意图，如图所示：
由不等式 xf（x）＜0可得，x与f（x）的符号相反，
结合图象可得不等式的解集为 {x|-5≤x＜-3，或 3＜x≤5}
故答案为[-5，-3）∪（3，5]．
解：由题意可得，函数的图象关于原点对称，在[-5，0）上是增函数，且f（3）=0，画出函数f（x）的单调性示意图，如图所示：
由不等式 xf（x）＜0可得，x与f（x）的符号相反，
结合图象可得不等式的解集为 {x|-5≤x＜-3，或 3＜x≤5}
故答案为[-5，-3）∪（3，5]．
点评：本题主要考查函数的奇偶性的应用，解不等式，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
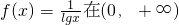是减函数；
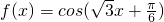，则f（x）+f'（x）是奇函数；
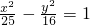的一个焦点到渐近线的距离是5；
是减函数；
，则f（x）+f'（x）是奇函数；
的一个焦点到渐近线的距离是5；