题目内容

（2012•济南三模）已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）和直线L：
x
a
-
y
b
=1，椭圆的离心率e=
6
3
，直线L与坐标原点的距离为
3
2
．
（1）求椭圆的方程；
（2）已知定点E（-1，0），若直线y=kx+2（k≠0）与椭圆相交于C、D两点，试判断是否存在k值，使以CD为直径的圆过定点E？若存在求出这个k值，若不存在说明理由．
分析：（1）利用直线L：
x
a
-
y
b
=1与坐标原点的距离为
3
2
，椭圆的离心率e=
6
3
，建立方程，求出椭圆的几何量，即可求得椭圆的方程；
（2）直线y=kx+2代入椭圆方程，利用韦达定理及CD为圆心的圆过点E，利用数量积为0，即可求得结论．
解答：解：（1）∵直线L：
x
a
-
y
b
=1与坐标原点的距离为
3
2
，∴
3
2
=
|ab|
a2+b2
．①…（2分）
∵椭圆的离心率e=
6
3
，∴
c2
a2
=
2
3
．②…（4分）
由①得4a2b2=3a2+3b2，即4a2（a2-c2）=3a2+3（a2-c2）③
由②③得a2=3，c2=2
∴b2=a2-c2=1
∴所求椭圆的方程是
x2 
3
+y2=1…（6分）
（2）直线y=kx+2代入椭圆方程，消去y可得：（1+3k2）x2+12kx+9=0
∴△=36k2-36＞0，∴k＞1或k＜-1…（8分）
设C（x1，y1），D（x2，y2），则有x1+x2=
-12k
1+3k2
，x1x2=
9
1+3k2
…（10分）
∵
EC
=(x1+1，y1)，
ED
=(x2+1，y2)，且以CD为圆心的圆过点E，
∴EC⊥ED…（12分）
∴（x1+1）（x2+1）+y1y2=0
∴（1+k2）x1x2+（2k+1）（x1+x2）+5=0
∴（1+k2）×
9
1+3k2
+（2k+1）×
-12k
1+3k2
+5=0，解得k=
7
6
＞1，
∴当k=
7
6
时以CD为直径的圆过定点E…（14分）
点评：本题考查椭圆的标准方程，考查椭圆的性质，考查直线与椭圆的位置关系，考查韦达定理的运用，考查向量知识，解题的关键是联立方程，利用韦达定理求解．
练习册系列答案
相关题目
（2012•济南三模）经市场调查，某旅游城市在过去的一个月内（以30天计），第t天（1≤t≤30，t∈N﹢）的旅游人数f（t） （万人）近似地满足f（t）=4+
1t
，而人均消费g（t）（元）近似地满足g（t）=120-|t-20|．
（1）求该城市的旅游日收益w（t）（万元）与时间t（1≤t≤30，t∈N﹢）的函数关系式；
（2）求该城市旅游日收益的最小值．
（2012•济南三模）某旅游景点预计2013年1月份起前x个月的旅游人数的和p（x）（单位：万人）与x的关系近似地满足p（x）=
1
2
x（x+1）•（39-2x），（x∈N*，且x≤12）．已知第x月的人均消费额q（x）（单位：元）与x的近似关系是q（x）=
35-2x(x∈N*，且1≤x≤6)
160
x
(x∈N*，且7≤x≤12)

（I）写出2013年第x月的旅游人数f（x）（单位：人）与x的函数关系式；
（II）试问2013年第几月旅游消费总额最大，最大月旅游消费总额为多少元？
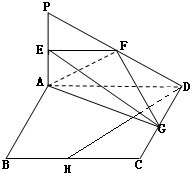（2012•济南三模）如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD，E、F、G、H分别是线段PA、PD、CD、BC的中点．
（Ⅰ）求证：BC∥平面EFG；
（Ⅱ）求证：DH⊥平面AEG；
（Ⅲ）求三棱锥E-AFG与四棱锥P-ABCD的体积比．
（2012•济南三模）已知直线l：y=x+1，圆O：x2+y2=
3
2
，直线l被圆截得的弦长与椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的短轴长相等，椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点M（0，-
1
3
）的动直线l交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得无论l如何转动，以AB为直径的圆恒过定点T？若存在，求出点T的坐标；若不存在，请说明理由．
（2012•济南三模）设函数f（x）=x2-2（-1）klnx（k∈N*），f′（x）表示f（x）导函数．
（I）求函数f（x）的单调递增区间；
（Ⅱ）当k为偶数时，数列{an}满足a1=1，anf′(an)
=a
2
n+1
-3．证明：数列{
a
2
n
}中不存在成等差数列的三项；
（Ⅲ）当k为奇数时，设bn=
1
2
f′(n)-n，数列{bn}的前n项和为Sn，证明不等式(1+bn)
1
bn+1
＞e对一切正整数n均成立，并比较S2012-1与ln2012的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网