题目内容
过点P(4,4)且与双曲线
-
=1只有一个公共点的直线有
| x2 |
| 16 |
| y2 |
| 9 |
4
4
条.分析:分为三类考虑:直线的斜率不存在;与渐近线平行的直线;与左支相切,即可得到结论.
解答:解:当直线的斜率不存在时,直线的方程为x=4,满足题意
因为a=4,b=3,所以双曲线的渐近线方程为y=±
x,
则过P分别作出两条与渐近线平行的直线即与双曲线只有一个交点;
过点P还可以作一条与左支相切的直线,
故满足条件的直线共有4条.
故答案为:4
因为a=4,b=3,所以双曲线的渐近线方程为y=±
| 3 |
| 4 |
则过P分别作出两条与渐近线平行的直线即与双曲线只有一个交点;
过点P还可以作一条与左支相切的直线,
故满足条件的直线共有4条.
故答案为:4
点评:本题考查了直线与双曲线有一个公共点的情况,做题时极容易丢平行渐近线的情况,做题时一定要细心.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
过点P(4,4)且与双曲线
-
=1只有一个交点的直线有( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、1条 | B、2条 | C、3条 | D、4条 |
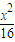 -
-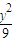 =1只有一个交点的直线有( )
=1只有一个交点的直线有( )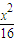 -
-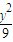 =1只有一个交点的直线有( )
=1只有一个交点的直线有( )