题目内容
若不等式ax2+bx+c>0的解集是{x|-1<x<3},且ax2+bx+c>1的解集是空集,则a的取值范围是 .
【答案】分析:由不等式ax2+bx+c>0的解集为{x|-1<x<3},根据三个二次之间的对应关系,我们易得a,b,c的关系,代入不等式ax2+bx+c>1结合其解空集易解出a的取值范围.
解答:解:∵不等式ax2+bx+c>0的解集是{x|-1<x<3},
∴ax2+bx+c=0的根为3、-1,
即3-2=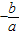
-3×1=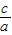
解得b=-a,c=-3a
则不等式ax2+bx+c>1可化为:
ax2-ax-3a-1>0
∴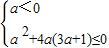
解得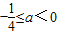
故答案为: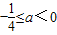
点评:本题考查的知识点是一元二次不等式的解法,及三个二次之间的关系,其中根据三个二次之间的关系求出a,b,c的关系,是解答本题的关键.
解答:解:∵不等式ax2+bx+c>0的解集是{x|-1<x<3},
∴ax2+bx+c=0的根为3、-1,
即3-2=
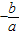
-3×1=
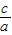
解得b=-a,c=-3a
则不等式ax2+bx+c>1可化为:
ax2-ax-3a-1>0
∴
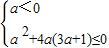
解得
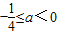
故答案为:
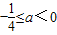
点评:本题考查的知识点是一元二次不等式的解法,及三个二次之间的关系,其中根据三个二次之间的关系求出a,b,c的关系,是解答本题的关键.

练习册系列答案
相关题目