Question

（本小题满分10分）

已知圆O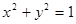：，圆C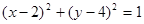：，由两圆外一点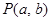引两圆切线PA、PB，切点分别为A、B，满足|PA|=|PB|.

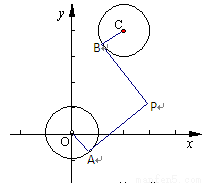
（Ⅰ）求实数a、b间满足的等量关系；

（Ⅱ）求切线长|PA|的最小值；

（Ⅲ）是否存在以P为圆心的圆，使它与圆O相内切并且与圆C相外切？若存在，求出圆P的方程；若不存在，说明理由.

 

Answer 1

【答案】

(1) (2)2(3)不存在符合题设条件的圆P

【解析】

试题分析：（Ⅰ）连结PO、PC，∵|PA|=|PB|，|OA|=|CB|=1，

∴|PO|²=|PC|²，从而

化简得实数a、b间满足的等量关系为：

.                            ………………3分

（Ⅱ）由，得

∴当时，                  ………………3分

（Ⅱ）∵圆O和圆C的半径均为1，若存在半径为R圆P，与圆O相内切

并且与圆C相外切，则有

  且 

于是有：  即 

从而得

两边平方，整理得   ……………2分

将代入上式得：

故满足条件的实数a、b不存在，∴不存在符合题设条件的圆P………………2分

考点：本试题考查了直线与圆的位置关系的运用。

点评：利用线与圆的相切，根据切线长定理建立关系式，进而得到a,b的关系。对于条件性探索试题，可以先假设存在，在假设的基础上推理论证，求解得到， 说明存在，不存在会找到一个矛盾。属于中档题。