题目内容
已知数列{an}前n项和为Sn,此无穷数列对于不小于2的正整数n,满足1-Sn=an-1-an.(1)求a1,a2,a3;
(2)证明{an}为等比数列;
(3)设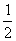 ,求
,求![]() (b1+b2+…+bn)的值.
(b1+b2+…+bn)的值.
(1)解析:∵S2=a1+a2,?
∴1-(a1+a2)=a1-a2,?
解得a1=![]() .?
.?
∵S3=a1+a2+a3,?
同理解得a2=![]() ,a3=
,a3=![]() .?
.?
(2)证明:当n≥2时,1-Sn=an-1-an. ①?
1-Sn+1=an-an+1 . ②?
①-②得Sn+1-Sn=an-1-2an+an+1 ,?
∴an+1 =an-1 -2an+an+1 .?
∴![]() ,?
,?
即![]() .?
.?
∴{an}为等比数列.?
(3)解析:∵bn=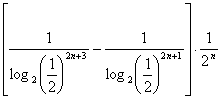 ?
?
![]()
![]() ,?
,?
∴![]() (b1+b2+…+bn)?
(b1+b2+…+bn)?
=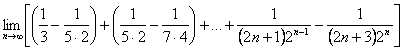
= .
.

练习册系列答案
相关题目