题目内容
若全集U=R，不等式
|
分析：把已知不等式的左边的行列式化简，得出一个二次不等式，进而求出不等式的解集即可得到集合A即可．
解答：解：由不等式
＞0，
变形为：x2-2x＞0，
化为：x（x-2）＞0，
解得：x＞2或x＜0．
所以集合A=（-∞，0）∪（2，+∞）
故答案为：=（-∞，0）∪（2，+∞）
|
变形为：x2-2x＞0，
化为：x（x-2）＞0，
解得：x＞2或x＜0．
所以集合A=（-∞，0）∪（2，+∞）
故答案为：=（-∞，0）∪（2，+∞）
点评：此题属于以不等式的解集为平台，考查了行列式的运算及转化的思想，是一道基础题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
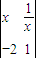（x＞0）的值域为集合A，
]，不等式f（x）+a≥0恒成立，求实数a的范围；
•
的值．
＞0的解集为A，则 A= ．
＞0的解集为A，则 A= ．