题目内容
（本小题满分12分）设递增等比数列{
}的前n项和为
，且
＝3，
＝13，数列{
}满足
＝
，点P（，
）在直线x－y＋2＝0上，n∈N﹡
（Ⅰ）求数列{
}，{}的通项公式
（Ⅱ）设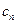
＝
，数列{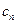}的前n项和
，若>2a－1恒成立（n∈N﹡），求实数a的取值范围．
解：（Ⅰ）由
可得
，
因为数列
为递增等比数列，所以
，
.
故是首项为
，公比为
的等比数列. 所以
.…………3分
由点
在直线
上，所以
.
则数列
是首项为1，公差为2的等差数列.则
. ………5分
（Ⅱ）因为
，所以
.
则
,………………………7分
两式相减得：
…………8分
所以
. ………………………………9分
. 若
恒成立，则
,
. ……………12分
解析
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
