题目内容
已知等差数列{an}中，a1=1，a3=-3，
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)若数列{an}的前k项和Sk=-35，求k的值．
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)若数列{an}的前k项和Sk=-35，求k的值．
解：(Ⅰ)设等差数列{an}的公差为d，则an=a1+(n-1)d，
由a1=1，a3=-3可得1+2d=-3，解得d=-2，
从而，an=1+(n-1)×(-2)=3-2n。
(Ⅱ)由(Ⅰ)可知an=3-2n，所以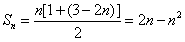
，
进而由Sk=-35可得2k-k2=-35，
即k2-2k-35=0，解得k=7或k=-5，
又k∈N*，故k=7为所求．
由a1=1，a3=-3可得1+2d=-3，解得d=-2，
从而，an=1+(n-1)×(-2)=3-2n。
(Ⅱ)由(Ⅰ)可知an=3-2n，所以
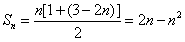，进而由Sk=-35可得2k-k2=-35，
即k2-2k-35=0，解得k=7或k=-5，
又k∈N*，故k=7为所求．
练习册系列答案
相关题目
已知等差数列{an}中，a4a6=-4，a2+a8=0，n∈N*．