题目内容
(本题满分12分)对于函数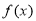 ,若存在
,若存在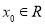 使得
使得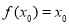 成立,则称
成立,则称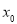 为
为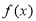 的不动点已知函数
的不动点已知函数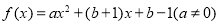
(1)若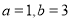 ,求函数
,求函数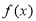 的不动点;
的不动点;
(2)若对任意实数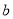 ,函数
,函数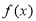 恒有两个相异的不动点,求
恒有两个相异的不动点,求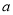 的取值范围;
的取值范围;
(3)在(2)的条件下,若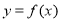 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数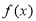 的不动点,且A、B两点关于直线
的不动点,且A、B两点关于直线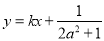 对称,求
对称,求 的最小值
的最小值
(1)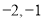
(2)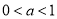
(3)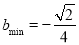
【解析】
试题分析:(1)解决本小题关键是理解不动点的含义,由题意可知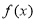 的不动点就是方程
的不动点就是方程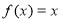 的根,因此第 (1)问可转化为求
的根,因此第 (1)问可转化为求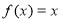 的根,第(2)问可转化为方程
的根,第(2)问可转化为方程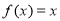 即
即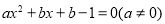 恒有两个不等实根,注意两次使用判别式才能求出
恒有两个不等实根,注意两次使用判别式才能求出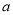 的取值范围.第(3)问与解析几何交汇,涉及到点关于直线对称问题,由A、B两点关于直线
的取值范围.第(3)问与解析几何交汇,涉及到点关于直线对称问题,由A、B两点关于直线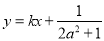 对称,可得
对称,可得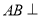 直线且中点
直线且中点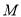 在直线上,由这两个条件可得
在直线上,由这两个条件可得 ,再利用函数求最值的方法求
,再利用函数求最值的方法求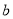 的最小值.
的最小值.
试题解析:
(1)若 ,
,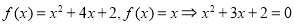 ,
,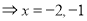 ,则
,则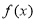 的不动点为
的不动点为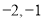 (2分)
(2分)
(2)函数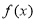 恒有两个相异的不动点,所以方程
恒有两个相异的不动点,所以方程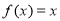 即
即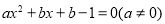 恒有两个不等实根,
恒有两个不等实根,
需要判别式大于0恒成立,即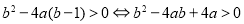 对任意实数
对任意实数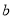 恒成立,
恒成立,
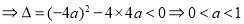 ,所以
,所以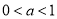 (6分)
(6分)
(3)因为A、B两点关于直线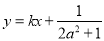 对称,所以
对称,所以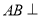 直线且中点
直线且中点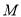 在直线上
在直线上
设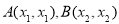 ,由(2)知,
,由(2)知,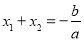
所以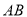 的中点
的中点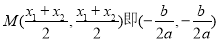
易知
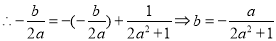
由(2),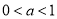 所以
所以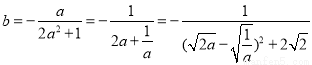
当且仅当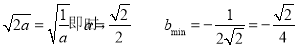 (12分)
(12分)
考点:1一元二次方程;2一元二次不等式恒成立;3点关于直线对称;4函数最值的求法.
考点分析: 考点1:函数的综合应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,则该椭圆的方程为( )
,则该椭圆的方程为( ) B.
B. C.
C. D.
D.
 的零点个数为( )
的零点个数为( ) ,
, ,
, ,则
,则 与
与 夹角的度数为 .
夹角的度数为 . 是( )
是( )
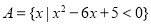 ,
, ,
,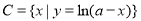 ,全集为实数集
,全集为实数集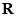
 ;
;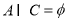 ,求实数
,求实数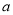 的范围[来源:学
的范围[来源:学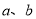 分别是方程
分别是方程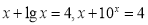 的解,
的解, 则关于
则关于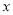 的方程
的方程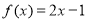 的解的个数是( )
的解的个数是( ) 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是 .
的解集是 .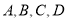 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求