Question

20070405

已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC = AD = CD = DE = 2a，AB = a，F为CD的中点.

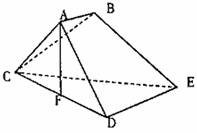
   （Ⅰ）求证：AF⊥平面CDE；

   （Ⅱ）求异面直线AC，BE所成角余弦值；

   （Ⅲ）求面ACD和面BCE所成二面角的大小.

Answer 1

解：（Ⅰ）∵DE⊥平面ACD，AF平面ACD

∴DE⊥AF

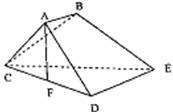又∵AC=AD=C，F为CD中点

∴AF⊥CD，

∴AF⊥面CDE

∴AF⊥平面CDE 

   （Ⅱ）∵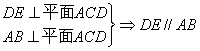

取DE中点M，连结AM、CM，则四边形AMEB为平行四边形

AM//BE，则∠CAM为AC与BE所成的角

在△ACM中，AC=2a

由余弦定理得：

∴异面直线AC、AE所成的角的余弦值为

   （Ⅲ）延长DA。EB交于点G，连结CG

因为AB//DE，AB=DE，所以A为GD中点

又因为F为CD中点，所以CG//AF

因为AF⊥平面CDE，所以CG⊥平面CDE

故∠DCE为面ACD和面BCE所成二面角的平面角

易求∠DCE=45°