题目内容
(本小题满分12分)已知两点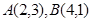 ,直线
,直线 ,在直线
,在直线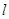 上求一点
上求一点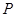 .
.
(1)使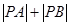 最小; (2)使
最小; (2)使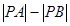 最大.
最大.
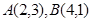 ,直线
,直线 ,在直线
,在直线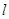 上求一点
上求一点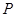 .
.(1)使
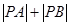 最小; (2)使
最小; (2)使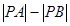 最大.
最大. (1)直线A1B与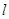 的交点可求得为
的交点可求得为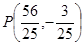 ,由平面几何知识可知
,由平面几何知识可知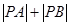 最小.(2)直线AB与
最小.(2)直线AB与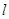 的交点可求得为
的交点可求得为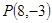 ,它使
,它使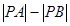 最大.
最大.
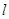 的交点可求得为
的交点可求得为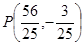 ,由平面几何知识可知
,由平面几何知识可知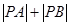 最小.(2)直线AB与
最小.(2)直线AB与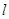 的交点可求得为
的交点可求得为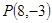 ,它使
,它使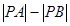 最大.
最大.试题分析:(1)要使得点P到点A,B的距离和最小,则利用两边之和大于等于第三边,结合对称性,做一个点A,(或者B)的关于直线的对称点A’(,或者B’),然后连接A’B与直线相交的交点即为所求的最小值的点P的位置。通过等价转化得到结论。
(2)而要求解
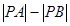 的最大值,则利用两点在直线的同侧,可以连线,延长与直线相交,结合两边之差小于等于第三边,当三点共线的时候满足最大值得到结论。
的最大值,则利用两点在直线的同侧,可以连线,延长与直线相交,结合两边之差小于等于第三边,当三点共线的时候满足最大值得到结论。解:(1)可判断A、B在直线l的同侧,设A点关于
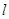 的对称点A1的坐标为(x1,y1).
的对称点A1的坐标为(x1,y1).则有
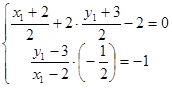 ﹍﹍﹍﹍﹍2分
﹍﹍﹍﹍﹍2分 解得
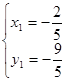 ﹍﹍﹍﹍4分
﹍﹍﹍﹍4分由两点式求得直线A1B的方程为
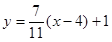 , ﹍﹍﹍﹍5分
, ﹍﹍﹍﹍5分直线A1B与
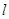 的交点可求得为
的交点可求得为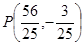 ﹍﹍﹍﹍6分
﹍﹍﹍﹍6分由平面几何知识可知
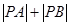 最小.
最小.(2)由两点式求得直线AB的方程
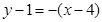 ,即
,即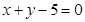 .﹍﹍﹍﹍8分
.﹍﹍﹍﹍8分直线AB与
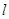 的交点可求得为
的交点可求得为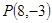 ,它使
,它使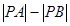 最大. ﹍﹍﹍﹍12分
最大. ﹍﹍﹍﹍12分点评:解决该类最值问题,一般要转换为三点共线的特殊情况来得到。

练习册系列答案
相关题目
 的最小值.
的最小值. 轴上的截距为2且倾斜角为135°的直线方程为 ( )
轴上的截距为2且倾斜角为135°的直线方程为 ( ) :2x+3y-1=0,
:2x+3y-1=0, :Ax-6y+C=0,当A,C满足条件:__________时,
:Ax-6y+C=0,当A,C满足条件:__________时, 方程为
方程为 ,且在
,且在 轴上的截距为
轴上的截距为 ,在
,在 轴上的截距为
轴上的截距为 ,则
,则 等于( )
等于( )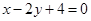 与直线
与直线 的交点,且与点A(0,4)和点B(4,O)距离相等的直线方程.
的交点,且与点A(0,4)和点B(4,O)距离相等的直线方程.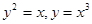 围成的封闭图形面积为____.
围成的封闭图形面积为____. ,直线
,直线 必经过的定点是
必经过的定点是



 0的两侧,则a的取值范围是 .
0的两侧,则a的取值范围是 .