题目内容

14．若二项式（x2-$\frac{2}{x}$）n展开式的第5项是常数项，则展开式的中间项为（　　）
A．-160B．-160x3C．20D．160x3

分析 根据二项式（x2-$\frac{2}{x}$）n展开式的第5项是T5=${C}_{n}^{4}$•（-2）4•x2n-12 为常数项，求得n=6，可得展开式的中间项．

解答 解：由于二项式（x2-$\frac{2}{x}$）n展开式的第5项是T5=${C}_{n}^{4}$•（-2）4•x2n-12 为常数项，
故2n-12=0，∴n=6，故展开式的中间项为T4=${C}_{6}^{3}$•（-2）3•x3=-160x3，
故选：B．

点评 本题主要考查二项式定理的应用，二项展开式的通项公式，属于基础题．

练习册系列答案
相关题目
4．已知函数f（x）=alog2x+blog3x+2，且f（$\frac{1}{2015}$）=-1，则f（2015）=（　　）
A．2B．3C．4D．5
5．数列{an}为等差数列，已知a3+2a8+a9=20，则a7=5．
2．已知y=log3（3x+1）+ax是偶函数，y=b+$\frac{2}{{e}^{x}-1}$为奇函数，则a+b=（　　）
A．-1B．0C．$\frac{1}{2}$D．1
9．已知平面内互不相等的非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°，则$\overrightarrow{a}$•$\overrightarrow{b}$的最大值为（　　）
A．2B．$\sqrt{3}$C．$\frac{3}{2}$D．$\frac{\sqrt{3}}{2}$
19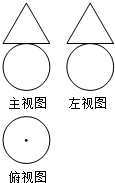．某几何体的三视图如图所示，其中三角形的三边长与圆的直径均为2，则该几何体的表面积为（　　）
A．$\frac{4+\sqrt{3}}{3}$πB．5πC．6πD．7π
6．在锐角△ABC中，三角形内角A，B，C所对的边分别为a，b，c，设$\overrightarrow{m}$=（cosA，sinA），$\overrightarrow{n}$=（cosA，-sinA），a=$\sqrt{7}$，且$\overrightarrow{m}•\overrightarrow{n}$=-$\frac{1}{2}$
（1）若b=3，求△ABC的面积；
（2）求b+c的最大值．
3．若曲线y=e-ax+1在点（0，2）处的切线与直线x+2y-1=0垂直，则a=（　　）
A．-2B．2C．-$\frac{2}{3}$D．$\frac{2}{3}$
4．过点M（2，1）且斜率为1的直线与抛物线y2=2px（p＞0）交于A，B两点，且M为AB的中点，则p的值为（　　）
A．$\frac{1}{2}$B．1C．$\frac{3}{2}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网