题目内容
用数学归纳法证明下面的等式
12-22+32-42+…+(-1)n-1·n2=(-1)n-1·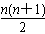 。
。
12-22+32-42+…+(-1)n-1·n2=(-1)n-1·
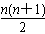 。
。解:(1)当n=1时,左边=12=1
右边=(-1)0·
∴原等式成立。
(2)假设n=k(k∈N*,k≥1)时,等式成立,
即有12-22+32-42+…+(-1)k-1·k2=(-1)k-1·
那么,当n=k+1时,则有
12-22+32-42+…+(-1)k-1·k2+(-1)k(k+1)2
=(-1)k-1· +(-1)k·(k+1)2
+(-1)k·(k+1)2


∴n=k+1时,等式也成立,
由(1)(2)得对任意n∈N*有
12-22+32-42+…+(-1)n-1·n2=(-1)n-1· 。
。
右边=(-1)0·

∴原等式成立。
(2)假设n=k(k∈N*,k≥1)时,等式成立,
即有12-22+32-42+…+(-1)k-1·k2=(-1)k-1·

那么,当n=k+1时,则有
12-22+32-42+…+(-1)k-1·k2+(-1)k(k+1)2
=(-1)k-1·
 +(-1)k·(k+1)2
+(-1)k·(k+1)2

∴n=k+1时,等式也成立,
由(1)(2)得对任意n∈N*有
12-22+32-42+…+(-1)n-1·n2=(-1)n-1·
 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,(其中
,(其中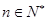 )
) 及
及 ;
; 与
与 的大小,并说明理由.
的大小,并说明理由. ,则
,则 ;
…………1分
;
…………1分
 ,则
,则 得到结论
得到结论 与
与 的大小,归纳猜想可得结论当
的大小,归纳猜想可得结论当 时,
时, ;
; 时,
时, ;
; 时,
时, ;
;
 时,
时, ,
, 时结论成立,
时结论成立, 时结论成立,即
时结论成立,即 ,
, 时,
时,


 ;
; ;
; 时,
时,