题目内容
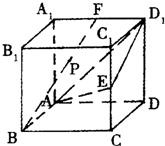如图，在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别是棱CC1，A1D1的中点．（1）证明：BF∥平面AED1；
（2）P为BF上异于F的任意一点，求证：PF⊥AE．
分析：（1）先取AA1中点G，连接FG，BG，则有FG∥AD1，BG∥ED1；进而得到平面BFG∥平面AED1，即可证明结论；
（2）先连接BD，FD，根据BD⊥平面ACE⇒BD⊥AE；再取D1D中点H，证明AE⊥平面BFD，即可得到想要证明的结论．
（2）先连接BD，FD，根据BD⊥平面ACE⇒BD⊥AE；再取D1D中点H，证明AE⊥平面BFD，即可得到想要证明的结论．
解答：证明：（1）取AA1中点G，连接FG，BG，则有FG∥AD1，BG∥ED1
又BG∩FG=G，∴平面BFG∥平面AED1，BF?平面BFG，
∴BF∥平面AED1．
（2）连接BD，FD，则BD⊥AC，BD⊥EC，EC∩AC=C，
∴BD⊥平面ACE，AE?平面ACE，
∴BD⊥AE．
取D1D中点H，连接AH，EH，可得FD⊥AH，FD⊥EH，EH∩AH=H，⇒FD⊥平面AEH．
AE?平面AEH，∴AE⊥FD，BD∩FD=D，
∴AE⊥平面BFD，BF?平面BFD，
∴AE⊥BF，P为BF上任一点，
∴AE⊥PF．
又BG∩FG=G，∴平面BFG∥平面AED1，BF?平面BFG，
∴BF∥平面AED1．
（2）连接BD，FD，则BD⊥AC，BD⊥EC，EC∩AC=C，
∴BD⊥平面ACE，AE?平面ACE，
∴BD⊥AE．
取D1D中点H，连接AH，EH，可得FD⊥AH，FD⊥EH，EH∩AH=H，⇒FD⊥平面AEH．
AE?平面AEH，∴AE⊥FD，BD∩FD=D，
∴AE⊥平面BFD，BF?平面BFD，
∴AE⊥BF，P为BF上任一点，
∴AE⊥PF．
点评：本题主要考查线面平行以及线线垂直．在证明线线垂直时，一般转化为证线面垂直．
练习册系列答案
相关题目
如图，在棱长为2的正四面体A-BCD中，若以△ABC为视角正面，则其正视图的面积是（ ）
