题目内容
设非零向量 与
与 的夹角为θ,
的夹角为θ, ,如果关于x的方程
,如果关于x的方程 有实根,那么θ的范围是 .
有实根,那么θ的范围是 .
【答案】分析:由已知中非零向量 与
与 的夹角为θ,
的夹角为θ, ,关于x的方程
,关于x的方程 有实根,我们可以构造一个关于
有实根,我们可以构造一个关于 与
与 的夹角θ的三角形不等式,解不等式可以确定cosθ的范围,进而得到的θ的范围.
的夹角θ的三角形不等式,解不等式可以确定cosθ的范围,进而得到的θ的范围.
解答:解:∵关于x的方程 有实根,
有实根,
∴ -4
-4 ≥0
≥0
即 -|
-| |•|
|•| |cosθ=
|cosθ= -
- |
| |2cosθ≥0
|2cosθ≥0
∴cosθ≤
故θ的范围是[45°,180°].
故答案为:[45°,180°].
点评:本题考查的知识点是数量积表示两个向量的夹角,一元二次方程根的个数与系数的关系,其中根据已知条件,构造关于 与
与 的夹角θ的三角形不等式,是解答本题的关键.
的夹角θ的三角形不等式,是解答本题的关键.
 与
与 的夹角为θ,
的夹角为θ, ,关于x的方程
,关于x的方程 有实根,我们可以构造一个关于
有实根,我们可以构造一个关于 与
与 的夹角θ的三角形不等式,解不等式可以确定cosθ的范围,进而得到的θ的范围.
的夹角θ的三角形不等式,解不等式可以确定cosθ的范围,进而得到的θ的范围.解答:解:∵关于x的方程
 有实根,
有实根,∴
 -4
-4 ≥0
≥0即
 -|
-| |•|
|•| |cosθ=
|cosθ= -
- |
| |2cosθ≥0
|2cosθ≥0∴cosθ≤

故θ的范围是[45°,180°].
故答案为:[45°,180°].
点评:本题考查的知识点是数量积表示两个向量的夹角,一元二次方程根的个数与系数的关系,其中根据已知条件,构造关于
 与
与 的夹角θ的三角形不等式,是解答本题的关键.
的夹角θ的三角形不等式,是解答本题的关键. 
练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 、
、 、
、 为非零向量,且
为非零向量,且 +
+ ,向量
,向量 ,
, ,则向量
,则向量 满足
满足

 。给出以下结论:
。给出以下结论: 是等差数列,2。
是等差数列,2。 ;3。设
;3。设 ,则数列
,则数列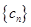 的前n项和为
的前n项和为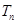 ,当且仅当n=2时,
,当且仅当n=2时, 与
与 的夹角为
的夹角为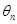 (
( ),均有
),均有 。其中所有正确结论的序号是____
。其中所有正确结论的序号是____ ,
, ,若向量
,若向量 与
与 的夹角为锐角,则实
的夹角为锐角,则实 的取值范围是
.
的取值范围是
.
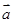 、
、 、
、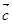 满足
满足 ,设向量
,设向量 ,则
,则