题目内容
“-2<m<1”是方程
+
=1表示椭圆的( )
| x2 |
| m+2 |
| y2 |
| 1-m |
| A、充分必要条件 |
| B、充分但不必要条件 |
| C、必要但不充分条件 |
| D、既不充分也不必要条件 |
分析:由题意要判断“-2<m<1”是方程
+
=1表示椭圆的什么条件等价于判断以下两个命题①若-2<m<1,则方程
+
=1表示椭圆;对于①有m的取值范围代入椭圆方程发现当m=-
时此方程表示圆与题意矛盾;
②若方程
+
=1表示椭圆,则-2<m<1的真假即可,也即利用所学的方程表示椭圆的充要条件进而判断出正误.
| x2 |
| m+2 |
| y2 |
| 1-m |
| x2 |
| m+2 |
| y2 |
| 1-m |
| 1 |
| 2 |
②若方程
| x2 |
| m+2 |
| y2 |
| 1-m |
解答:解:由题意“-2<m<1”是方程
+
=1中的m+2>0且1-m>0但是当m=-
时,m+2=1-m,此时方程表示圆而非椭圆,所以命题①为假命题,
又由于若方程
+
=1表示椭圆等价于:
?m∈(-2,-
)∪(-
,1),此时m的范围一定都在-2<m<1的范围内,所以命题②真确.
故“-2<m<1”是方程
+
=1表示椭圆的必要而不充分条件.
故选:C
| x2 |
| m+2 |
| y2 |
| 1-m |
| 1 |
| 2 |
又由于若方程
| x2 |
| m+2 |
| y2 |
| 1-m |
|
| 1 |
| 2 |
| 1 |
| 2 |
故“-2<m<1”是方程
| x2 |
| m+2 |
| y2 |
| 1-m |
故选:C
点评:此题考查了充分条件,必要条件及其判断方式,还考查了椭圆的标准方程及不等式的求解,此题主要考查课学生做题时的细心程度.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
(2009•普宁市模拟)为了确保神州七号飞船发射时的信息安全,信息须加密传输,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
|
 给出下列四个命题:
给出下列四个命题: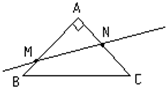 如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分. ;
; ,则α+β=1是A、B、C三点共线的充要条件;
,则α+β=1是A、B、C三点共线的充要条件; (p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
(p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;


