题目内容
已知函数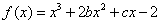 的图象在与
的图象在与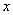 轴交点处的切线方程是
轴交点处的切线方程是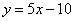 .
.
(Ⅰ)求函数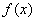 的解析式;
的解析式;
(Ⅱ)设函数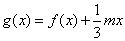 ,若
,若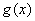 的极值存在,求实数
的极值存在,求实数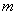 的取值范围以及当
的取值范围以及当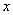 取何值时函数
取何值时函数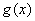 分别取得极大和极小值.
分别取得极大和极小值.
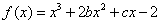 的图象在与
的图象在与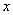 轴交点处的切线方程是
轴交点处的切线方程是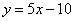 .
.(Ⅰ)求函数
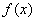 的解析式;
的解析式;(Ⅱ)设函数
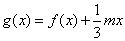 ,若
,若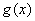 的极值存在,求实数
的极值存在,求实数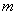 的取值范围以及当
的取值范围以及当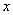 取何值时函数
取何值时函数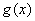 分别取得极大和极小值.
分别取得极大和极小值.(1)
(2)当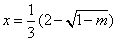 时
时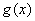 有极大值;
有极大值;
当 时
时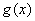 有极小值
有极小值

(2)当
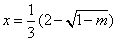 时
时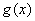 有极大值;
有极大值;当
 时
时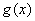 有极小值
有极小值试题分析:解:(1)由已知,切点为
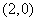 ,故有
,故有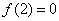 ,
,即
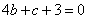 ① 1分
① 1分又
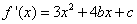 ,由已知,
,由已知, 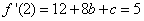 .
.得
 ② 3分
② 3分联立①②,解得
 ,
,于是函数解析式为
 5分
5分(2)
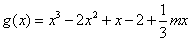 ,
,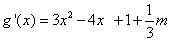 ,令
,令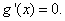 6分
6分当函数有极值时,方程
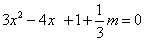 必有实根,
必有实根,由
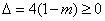 ,得
,得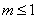 . 8分
. 8分①当
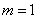 时,
时, 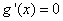 有实根
有实根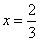 ,在
,在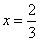 左右两侧均有
左右两侧均有 ,故函数
,故函数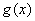 无极值.
无极值.②当
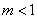 时,
时, 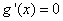 有两个实根,
有两个实根, 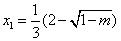 ,
, 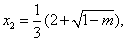
当
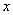 变化时,
变化时, 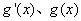 的变化情况如下表:
的变化情况如下表:| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
故当
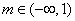 时,函数
时,函数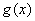 有极值:当
有极值:当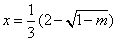 时
时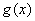 有极大值;
有极大值;当
 时
时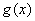 有极小值. 12分
有极小值. 12分点评:主要是考查了导数在研究函数中的运用,属于基础题。

练习册系列答案
相关题目
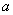 是实数.若函数
是实数.若函数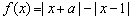 是定义在
是定义在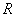 上的奇函数,但不是偶函数,则函数
上的奇函数,但不是偶函数,则函数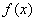 的递增区间为__________;
的递增区间为__________; 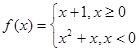 的零点的个数为 .
的零点的个数为 .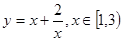 的值域为 .
的值域为 .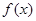 满足对于
满足对于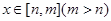 时有
时有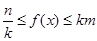 恒成立,则称函数
恒成立,则称函数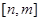 上是“被k限制”,若函数
上是“被k限制”,若函数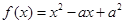 在区间
在区间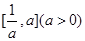 上是“被2限制”的,则
上是“被2限制”的,则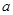 的取值范围为 .
的取值范围为 .
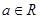
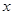 的不等式
的不等式 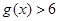
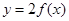 的图象恒在函数
的图象恒在函数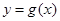 的上方,求实数
的上方,求实数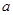 的取值范围。
的取值范围。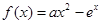
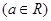 .
.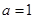 时,证明:
时,证明: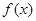 在
在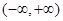 上为减函数;
上为减函数;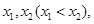 求实数
求实数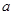 的取值范围.
的取值范围.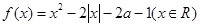 有四个不同的零点,则实数
有四个不同的零点,则实数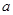 的取值范围是_______________.
的取值范围是_______________.