题目内容

A={x|（x-1）²＜3x-7}，则A∩Z的元素的个数 ________．

0
分析：化简集合A到最简形式，发现A=∅，故A∩Z=∅，进而可得答案．
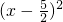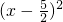解答：A={x|（x-1）²＜3x-7}={x|x²-5x+8＜0}={x|x²-5x+8＜0}={x| $\text{[math]}$ + $\text{[math]}$ ＜0}=∅，
∵∅中不含任何元素，元素的个数是0，
∴A∩Z=∅，A∩Z 的元素的个数是0，
故答案为0．
点评：本题考查一元二次不等式的解法，以及求2个集合的交集．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知函数f（x）的图象在[a，b]上连续不断，定义：f₁（x）=min{f（t）|a≤t≤x}（x∈[a，b]），f₂（x）=max{f（t）|a≤t≤x}（x∈[a，b]），其中，min{f（x）|x∈D}表示函数f（x）在D上的最小值，max{f（x）|x∈D}表示函数f（x）在D上的最大值，若存在最小正整数k，使得f₂（x）-f₁（x）≤k（x-a）对任意的x∈[a，b]成立，则称函数f（x）为[a，b]上的“k阶收缩函数”．已知函数f（x）=x²，（x∈[-1，4]）为[-1，4]上的“k阶收缩函数”，则k的取值是

（2012•河北模拟）设全集U=R，A={x|2(x-1)2＜2}，B={x|log

(x2+x+1)＞-log2(x2+2)}，则图中阴影部分表示的集合为（　　）

A．{x|1≤x＜2}

C．{x|0＜x≤1}

已知集合A={x|-x²+x+2＞0}，B={x|-1＜x＜1}，则A∩（?_UB）=（　　）

A．{x|1＜x＜2}

B．{x|-1＜x＜1}

C．{x|1≤x＜2}

D．{x|x＜1或x＞2}

集合A={x|-1≤x≤2}，B={x|x＜1}，则A∩B=（　　）

B．{x|-1≤x≤2}

C．{x|-1≤x≤1}

D．{x|-1≤x＜1}

已知下列四个命题：
①若函数y=f（x）在x_°处的导数f′（x₀）=0，则它在x=x₀处有极值；
②若不论m为何值，直线y=mx+1均与曲线

=1有公共点，则b≥1；
③若x、y、z∈R+，a=x+

，则a、b、c中至少有一个不小于2；
④若命题“存在x∈R，使得|x-a|+|x+1|≤2”是假命题，则|a+1|＞2；
以上四个命题正确的是

（填入相应序号）