题目内容
(本小题满分12分)
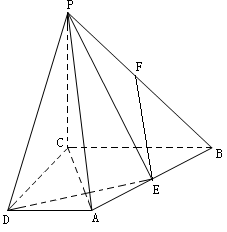 如图,四棱锥P-ABCD中,AD∥BC,∠ADC=
如图,四棱锥P-ABCD中,AD∥BC,∠ADC=![]() ,PC⊥平面ABCD,点E、F分别为AB、PB中点。AC⊥DE,
,PC⊥平面ABCD,点E、F分别为AB、PB中点。AC⊥DE,
其中AD=1,PC=2,CD=![]() ;
;
EF∥平面PAC;
求点B到平面PDE的距离。
(1)∵点E、F分别为AB、PB中点
∴EF为△BPA的中位线
∴EF∥PA
![]()
∵
∴EF∥平面PAC;
(2)PC⊥平面ABCD=>PC⊥DE
而已知有AC⊥DE
所以DE⊥平面PAC
又∵DE![]() 平面PDE
平面PDE
∴平面PDE⊥平面PCA
∵AE=EB,E![]() 平面PDE
平面PDE
∴点B到平面PDE的距离=点A到平面PDE的距离
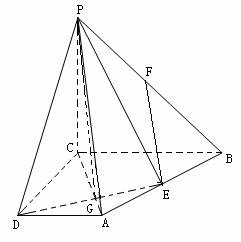
设AC交DE于G,连PG,则点A到PG的距离就是
点A到平面PDE的距离,也就是点B到平面PDE的距离。
由∠ADC=![]() ,AD=1,CD=
,AD=1,CD=![]() 得AC=2,AG=
得AC=2,AG=![]()
GC=![]() ,PG=
,PG=![]()
过A作AH⊥PG于H,则AH的长就是点B到平面PDE的距离,见下图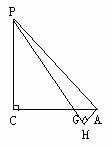
则△PCG∽△AHG
∴![]()
即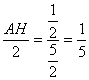
∴![]()

练习册系列答案
相关题目