题目内容
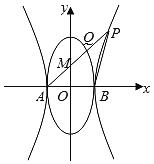
【题目】已知椭圆![]() ,直线l不经过坐标原点O且不平行与坐标轴,l与
,直线l不经过坐标原点O且不平行与坐标轴,l与![]() 相交于A,B两点,线段
相交于A,B两点,线段![]() 的中点为M.
的中点为M.
(1)证明:直线![]() 的斜率与直线l的斜率的乘积为定值;
的斜率与直线l的斜率的乘积为定值;
(2)若直线l过点![]() ,延长线
,延长线![]() 与
与![]() 交于点P,若四边形
交于点P,若四边形![]() 是平行四边形,求直线l的斜率;
是平行四边形,求直线l的斜率;
【答案】(1) 直线![]() 的斜率与直线l的斜率的乘积为定值
的斜率与直线l的斜率的乘积为定值![]() ;(2)
;(2)![]()
【解析】
(1)设点![]() ,再代入椭圆方程,相减后即可求得
,再代入椭圆方程,相减后即可求得![]() 的斜率与中点
的斜率与中点![]() 与
与![]() 的斜率.再化简证明乘积为定值即可.
的斜率.再化简证明乘积为定值即可.
(2) 点![]() ,再根据四边形
,再根据四边形![]() 是平行四边形可得
是平行四边形可得![]() 在椭圆上,进而求得
在椭圆上,进而求得![]() 的关系,再设直线
的关系,再设直线![]() 的方程
的方程![]() ,联立椭圆方程求
,联立椭圆方程求![]() 代入关系化简即可.
代入关系化简即可.
(1) 设![]() 且
且![]() ,则
,则![]() ,①
,①![]() ②,
②,
①-②得:![]() ,
,![]() ,
,
![]() .又
.又![]() ,
,
故![]() ,
,![]() ,
,
故直线![]() 的斜率与直线l的斜率的乘积为定值
的斜率与直线l的斜率的乘积为定值![]() .
.
(2)由题,因为四边形![]() 是平行四边形,故
是平行四边形,故![]() ,设
,设![]() 则
则![]() .又
.又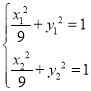 ,且
,且![]() .
.
故![]() ,化简得
,化简得![]() .
.
当直线![]() 斜率为0时, 四边形
斜率为0时, 四边形![]() 不是平行四边形.
不是平行四边形.
故设直线![]() 的方程
的方程![]() ,则
,则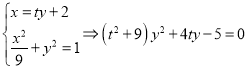 .
.
故![]() ,又
,又  .
.![]() .
.
故![]() ,故
,故![]() ,
,![]() .
.
故此时求直线l的斜率为![]()

练习册系列答案
相关题目