Question

已知函数f(x)=x(x-a)(x-b)，点A(m,f(m))，B(n,f(n)).

(1)设b=a，求函数f(x)的单调区间.

(2)若函数f(x)的导函数f′(x)满足：当|x|≤1时，有|f′(x)|≤恒成立，求函数f(x)的表达式

(3)若0＜a＜b，函数f(x)在x=m和x=n处取得极值，且a+b≤2.问：是否存在常数a,b，使得·=0?若存在，求出a,b的值；若不存在，请说明理由.

Answer 1

解:(1)f(x)=x³-2ax²+a²x,令f′(x)=3x²-4ax+a²=0，得x₁=，x₂=a.1°当a＞0时，x₁＜x₂.

∴所求单调增区间是(-∞,)，(a,+∞)，单调减区间是(，a).

2°当a＜0时，所求单调增区间是(-∞,a)，(,+∞)，单调减区间是(a，).

3°当a=0时，f′(x)=3x²≥0,所求单调增区间是(-∞,+∞).

(2)f(x)=x³-(a+b)x²+abx，∴f′(x)=3x²-2(a+b)x+ab.

∵当x∈［-1,1］时，恒有|f′(x)|≤,∴≤f′(1)≤,≤f′(-1)≤,≤f′(0)≤,

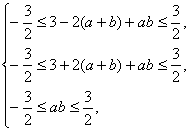即得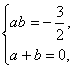

此时，满足当x∈［-1,1］时,|f′(x)|≤恒成立.∴f(x)=x³-x.

(3)存在a,b使得·=0.若·=0，即m·n+f(m)·f(n)=0,

∴mn+mn(m-a)(m-b)(n-a)(n-b)=0.

由于0＜a＜b，知mn≠0,∴(m-a)(m-b)(n-a)(n-b)=-1.①

由题设，m,n是f′(x)=0的两根,∴m+n=，mn=.②

②代入①得ab(a-b)²=9.

∴(a+b)²=(a-b)²+4ab=+4ab≥2=12，当且仅当ab=时取“=”.∴a+b≥2.

∵a+b≤2,∴a+b=2.又∵ab=，0＜a＜b,

∴a=，b=.